３０　光学過程と方違い

平安時代や室町時代には、ある目的地へ出発する日の方角が悪いと、その日の方角のよい方向にあるお寺などへ向かって宿泊し、そこから日を見計らって本来の目的地へ向かう「方違い」という習わしがありました。この習わしは、原子や分子の電子が、フォトンを吸収したり放出したりする光学過程を考える例えとして便利です。

次の絵は電子がiというエネルギー状態から別のｆという状態へ、フォトンを一個吸収したり（左側）、放出（発光）したり（右側）する光学過程を描いています。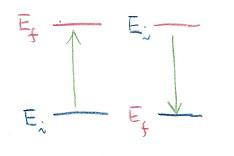横棒は電子の時間的に変化しない状態（定常状態と呼ばれます）のエネルギーの位置（準位と呼ばれます）で、上にあるほどエネルギーが高いことを表します。ここでE _i やE_ｆは_、次の時間を含まないシュレーディンガー方程式で得られる電子のエネルギー、E_ｊ（ｊ＝１～ｎ）の内の二つです。

ここでは水素原子の電子を例にとってきましたので、V_e-pは電子と陽子の間に働く引力のポテンシャルです。この図は、最初　i　の状態（始状態、initial state、と呼ばれます）にあった電子が、光と相互作用の結果最終的にｆの状態（終状態、final state、と呼ばれます）を持つような光学過程の内、もっとも単純なものを表しています。

このような光学過程が起きるかとか、どれほど起こりやすいかを知るには、電磁場が時間によって変化しますので、次の方程式を解いて考える必要があります。

ここで、V’は電子と電磁場との相互作用を表します。量子力学ではこの方程式を解くについて次のような方針をたてます。

電子が始状態から、電磁場と相互作用によって、終状態に変化すると考えるのですが、終状態は一般には特定できません。そこでとりあえず、どの状態にもなる確率があると考え、しかも、それぞれの状態へ変化する（遷移するといいます）確率は時間と共に変化していくと考えます。そして、そのような変化も含めた波動関数は次のように表現できると考えます。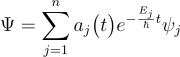　この記号はｊ＝１からｎまでについて足し合わせることを意味します。この式では定常状態の波動関数として、次の矢印の右側のようなものが選ばれます。　

その理由は、時間によって変化しない電子の波動関数は、もともとの次の方程式の右辺をEψとしたものの解です。

ですから、左辺についての方程式、の解でもあるからで、それから時間によって変動する指数関数の部分が付いたものが、ほんとうの解だからです。

このような波動関数の和を、電磁場との相互作用を含んだ方程式に代入して計算するのですが、これはｎ個のa(t)についての方程式が連立方程式になったようなもので、正確には解けません。ただ、計算しなくても、どのような光学現象が起きるかを推測できる量があります。これをMと呼ぶことにしますが、これについては、３０ーaで補足します。

上の絵の一個の矢印にそれ相応のMが対応することがわかっていて、その光学過程が起きるかとか、その効率はMの数値的な評価から知ることができます。しかし、その方法はかなり専門的なので、３０－aの補足でも、Mの特徴についてだけ触れますが、これだけでも光学過程の大筋を知るには十分だと思います。

次の絵は、もうすこし複雑な光学過程の例です。

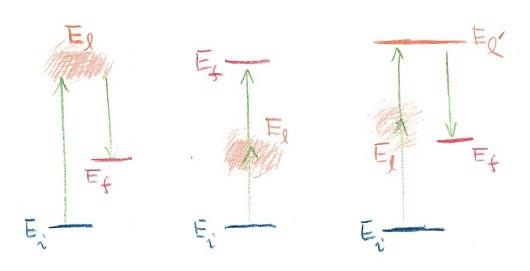
左の過程は二つの過程が引き続いて起きるもので、始状態の電子が光と相互作用してｌへ一旦遷移し、さらにｌからもう一度光と相互作用して最後に終状態ｆへ落ち着くという過程です。ここでｌという状態は中間状態といわれ、「方違い」の中継地のお寺のようなものです。

方違いの時には、彼らはそれなりに長くお寺に滞在したらしいのですが、光学過程では本当にそのお寺に泊まる必要はなく、泊ったつもりぐらいの非常に短い滞在時間だと考えられています。しかも、一か所のお寺である必要はなく、同時に無数のお寺に寄ったつもりでもOKなのです。

一般に、光学過程を理解する時には、一回の相互作用による効果（絵の一個の矢印）を一つの素過程として、それをレゴの部品のよう順次組み立てて一つながりの過程を扱うことができます。どのほどの効率でその光学過程が起きるかは、実際に計算しなければわかりませんが、レゴの部品の数が多いほどその現象は起こりにくいといえます。

もっと一般の複雑な量子過程では、数式で書くとますます面倒で長ったらしくなり、計算法もそれぞれの素過程でおおよそ決まっているので、図形で表現すると直観的に意味が分かるし、計算の手順もわかることをファイマン（Richard Phillips Feynman, 1918-1988）が気づき、今日ファイマンダイアグラムとして便宜的に広く使われています。今日世界的に使われるようになった、絵文字で重要なこと表現するようなものです。

絵の真ん中に示した過程は２光子過程と呼ばれるもので、この場合もどのような中間状態ｌを経由しているかは必ずしも明らかではありません。又、絵の右端の例は、さらに複雑なものですが、中間状態の中の特定のｌ’では、お寺の門をくぐってしまったような場合になり、電子は一泊することも、泊まらずにでていくこともできて、どっち付かずの状態が実際に起きます。このような状況で生まれる発光は共鳴蛍光と呼ばれ、最初の図で示した発光とはスペクトルの様子が違います。

シュレーディンガーは、最初の論文では具体的には示していなかったのですが、ボーアのいう光学遷移のミクロな光学過程を、以上のように彼の方程式から計算できることを彼はすでに見込んでいたわけです。

このようにシュレーディンガー方程式から色々なミクロな現象をが明らかにできるのですが、彼自身も波動関数というものを使えることの真意には納得できず、ボルンやボーアの主張する波動関数の確率的解釈には懐疑的でした。何故でしょう？　これがここでの次の課題です。