２６　シュレーディンガーのひらめき

ド・ブロイのアイデアを発展させて、ミクロな物体の持つ波の性質を表す波動方程式を導いたのは、オーストリアのシュレーディンガー（Erwin Rudolf Josef Alexander Schrödinger,　1887-1961）で、１９２６年のことです。この論文はアメリカの専門誌Phys.Rev.に発表されたもので、英文で書かれ、彼の理論の狙いや見通しなどが最初にまとめてあります。

彼の導いた波動方程式は、今日シュレーディンガー方程式と呼ばれ、原子や分子の構造や安定性、光との相互作用など、ミクロな世界（量子力学が必要になる世界）を理解するうえで基礎となる方程式で、マクロの世界のニュートンの運動方程式に対応するものです。ニュートンの力学は量子力学に対して古典力学とも呼ばれます。量子力学の教科書では、レベルに応じてさまざまなアプローチでこの方程式の説明がなされています。ここでは、彼がこの方程式に至る考えを思いついた動機と、これまでこのブログで使ってきた範囲の数学を使って、この方程式の原型を導き、それを彼が一般化したアイデアや、彼の目論んだこの方程式の可能性を、上の論文を基にメモすることにします。

まず、彼の動機ですが、１９１１年、イギリスのラザフォードたちは原子の中心には小さな芯があることを実験で発見しました。その２年後、デンマークのボーア（ Niels Henrik David Bohr、1885-1962)が、理論的に原子がそのような構造を保つための条件を提案しました。それによると、電子は速度ｖでその芯の周りの回っているとすると、電流が流れていると考えられるのですが、運動の向きが変わる、つまり加速度が生じているので、電子は電磁波を放出する（前に述べたラモーアの式を思い出してください）、そうすると電子のエネルギーは徐々に減っていくので、同じ軌道では運動できない。寿命が尽きた人工衛星が地上へ落ちてくるようなイメージです。

しかし、原子は電気的に中性だから、マイナスの電荷をもった電子は、中心にあるプラスの電荷によって引き寄せられるから、その引力が遠心力と釣り合う場合には、一定のエネルギーで周回を続けられる。その時は、ニュートン力学から、中心からの距離ｒにｍｖ（運動量と呼ばれます）をかけた量（角運動量と呼ばれます）が保存される。したがって、原子の中の電子の運動では、角運動量に対して、次のような数式が成り立っていると考えられるだろうと考えました。（ボーアの関係式）。　ここでｈはプランク定数、ｎは１，２，３、・・・という整数です。

一方、ド・ブロイは、前に述べたように電子には次の波長の波の性質があるとしました。　そこで、シュレーディンガーはピンと来たのでしょう。ド・ブロイの関係式の両辺をある長さaで割りますと、　となります。このようにすると、右辺の分母はボーアの関係式のｎ＝１に対応する半径ｒをaとしたものと同じです。その場合、となります。

そこでシュレーディンガーは、光の波長がスリットの幅の長さ程度になると、光には波としての性質がはっきりと表れる（回折が起きる）事実から類推して、原子のような小さな領域では、電子も波の性質を表すのだろう。それならその波を表す方程式ができるはずだと考えました。この発想は彼の最初の論文に書かれていて、なるほどそのように考えたのかと感心しました。

そうして彼はシュレーディンガー方程式の原型となる次の方程式を導きました。（簡単のために空間座標はｘだけにします）

この方程式の導き方の出発点は、次の３つの数式です。一つはプランクの仮説から、、次はド・ブロイの仮説から、、そして、　　です。

一方、一般的に波の振幅が従う波動方程式との関係をつけるために、次のような波を表す波動関数を想定します。ここで指数関数を使うのは、波動方程式を導く上で、前に述べたように、指数関数の微分は何次でも元の関数に比例するという特徴を使うためです。

しかし、ド・ブロイのいう波を普通の波と区別するために、Ψという字を使って表します。

まずこの関数を時間ｔで一度（偏）微分しますと、となります。ここで、振動数νをプランクの仮説からエネルギーEに換えて表現しました。

一方、今度はｘで（偏）微分しますと、となります。ここで波長λから波数ｋに換えて表現しました。更にもう一度ｘで微分しますと、となります。ここでは、ド・ブロイの仮説によって、波数ｋを運動量ｐに換えて表現しました。

次に前の式の両辺にiℏを掛けると、となります。一方、後の式の両辺に を掛けると、となります。そこで両方の式を比べると、であることがわかります。

これがシュレーディンガー方程式の原型ですが、重要なことは、このように得られた方程式が、現実の物理現象を説明できる保証はこの段階では全くないことです。これは単にド・ブロイの仮想的な波を表す方程式です。

シュレーディンガーの洞察の素晴らしさは、ここでEを運動エネルギー、　だけではなく、ポテンシャルエネルギーVを含めた全エネルギーだと拡張解釈してみたことです。

そうして、今日シュレーディンガー方程式と呼ばれる一般的な方程式を導きました。

ここで右辺の[ ]に囲んだ部分はHと書いてハミルトニアンと呼ばれます。その所以や[ ]の中の意味については、専門的になるのでここでは省略します。ここで重要なことは、エネルギーをV＝０の値を基準にして測ることにしたことです。これによって、この方程式が現実の物理現象を説明できる見通しが予測できることです。次の絵はV＞０かV＜０かでド・ブロイの波がどうなるかを描いたものです。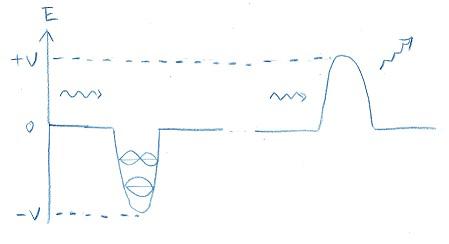

縦軸は、V＝０から測った量子（今の場合は一個の電子）の全エネルギー（運動エネルギー＋ポテンシャルエネルギー）を表します。ポテンシャルに関係なく電子が自由にある速さで運動しているときには、ド・ブロイの波は光でいえば平面波に対応します。

さて、V＜０の場合は左の場合で、原子の芯（原子核）のプラスの電荷との引力を受けている場合になり、ライオンが落とし穴に落ち込んだようになりますが、その時に波は、限られた空間に閉じ込められるので定在波になることが予想できます。一方、V>0なら、ライオンが何かにつまずいて曲がって走り去るようなもので、ド・ブロイの波は向きを変えて進みます。その時エネルギーを失えば非弾性散乱、変わらなければ弾性散乱です。

具体的に方程式を解くには、現実にどのようなポテンシャルの中での電子の運動を論じるかかが重要になります。しかし、実際の自然は複雑なので、物理学の常套手段は、まず、もっとも効果の大きそうなポテンシャルだけを選んで方程式解くことから始めます。そのため量子力学の教科書では、その出発点になる典型的なVの例について、それぞれの解法が説明されています。そうしてとりあえず求められた結果を実際と比べて不足が見つかると、少しずつ無視してきた効果を取り入れて補っていくわけです。したがって、ポテンシャルを決めた段階で、とりあえずの問題は解けたことになります。もっとも、その方程式が数学的に解けるかどうかは別の技術的な問題です。

さて、シュレーディンガーは、自分の理論の有効性を確かめるために、左の場合の典型的な例として、水素原子の電子の運動をこの方程式に当てはめて計算しました。

まず、ボーアの仮説に従うと、その条件を満たす電子は、時間的に変化しないので、次の式の左辺がゼロの場合を計算しました。

つまり、右辺の[ ]の中をEとして、時間によって変わらないEが求められるかを吟味したわけです。上の絵で想像できるように、多分Eはポテンシャルの穴の中に立ちうる定在波の数だけあるはずです。

なお、ここでもう一つ彼が目論んだ重要なことがあります。

ボーアは、原子の中の電子のエネルギーが不連続になるのにもかかわらず、原子は決まった波長の光を吸収したり発光したりするのは、あるエネルギーを持った電子が、違ったエネルギーを持った状態へ飛び移る（遷移すると呼ばれます）ものだと考えると、実際に観測される事実を説明できることを示しました。しかし、そのメカニズムを定量的に説明することはできませんでした。シュレーディンガーは上の方程式で左辺がゼロでない時間変化も含んだ方程式を解けば、そのメカニズムが定量的にわかると、具体的な計算法は抜きに上の論文で述べています。