３　励起子（exciton)

ポジトロニウムに似た励起子（exciton)というエキゾチック原子があります。これは半導体の結晶のような固体に適当な波長の光を照射すると生まれます。この量子は、電子と正孔が対となって結合したもので、光学的にはフォトン一個から生まれます。

この量子は１９３０年代にロシアのフレンケル（Yakov Il'ich Frenkel 1894-1952）が理論的に提案しました。　

この励起子は「フレンケル励起子」と呼ばれ、励起子の半径が原子や分子の大きさとそう変わらないほど小さい場合にいいモデルになります。

一方、半径が大きく、励起子の体積の中にたくさんの原子が含まれるほどの大きな励起子もあります。この励起子は、「ワニエ励起子」と呼ばれ、フレンケルより少し遅れてスイスのワニエ（Gregory Hugh Wannier ,1911-1983)が提唱しました。

「ワニエ励起子」の特徴は分光学的には実に見事な水素原子のようなスペクトルの系列が見られることで、固体物理の教科書では励起子の例としてよく紹介されています。

しかし、どちらも両極端なモデルで、実際は物質によって両者の性質が程度の差こそあれ混じっています。このブログでは簡単のために、ワニエ励起子が典型的に表れる半導体の結晶（塩化銅と亜酸化銅）を例として、その光学的性質を紹介します。

固体は膨大な数の原子が集まったものです。中でも結晶はそれらが周期的な構造を保っている巨大分子のようなものです。例えばダイヤモンドは原子番号１２の炭素原子だけが集まった結晶で、１カラット（０．２グラム）の結晶には、およそ0.017ｘ6.0ｘ10²³個の炭素原子が含まれます。また一個の炭素原子の電子の数も複数ですから、結晶全体の電子の数も膨大です。ですから、一個の水素原子の場合と違って、多数の電子同士の相互作用も考慮して、電子のエネルギー状態を理論的に正しく見積もることは困難で、いろいろな近似が必要になります。そのため詳し話は固体物理学の教科書に譲らざるを得ません。ただ、幸いなことに、ここで主に扱う半導体結晶では、比較的簡略な取り扱いが実際に使えます。その概略はこちらを参照してください。

次の図のAは、半導体結晶の電子のエネルギーの概略です。

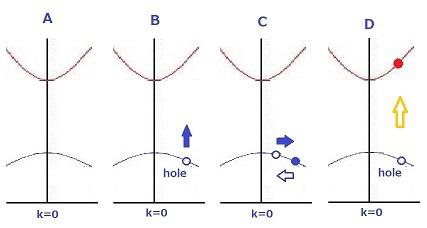上が伝導帯と呼ばれ、どの波数で表される量子状態（一個の水素原子では量子数でエネルギーを区別しますが、結晶では波数ｋが量子数の代わりになります）も空いています。波数がゼロの付近ではエネルギーは上に開いた放物線の形に見えますので、エネルギーεは、ε＝（ここで）と近似できます。この式のｍは質量の意味を持ちますが、物体の質量ではなく形式上の量ですので、伝導電子の有効質量と便宜的に呼んで、ｍ_eと書いておきます。

同様に下側の上に凸の放物線は価電子帯と呼ばれ、このすべての波数の状態は、パウリの排他律を反映して電子で埋まっていいます。このエネルギー帯では波数が大きいほどエネルギーが低くなりますので、有効質量は負の値を持ちます。

図のBは、価電子帯の一個の電子が何かの事情でなくなり、まるで全部つまっていた電子の状態の内の一個だけが抜けて、泡ができたようになったものです。この泡はプラスの電気を帯びて周りの電子を呼びよせ、その泡の位置に別の電子が入ると泡が移動します。その様子が図のCです。

このように、この泡は電子と逆の電荷を持ち常に電子と逆に行動し、エネルギーもマイナスの方向に加速される量子のような性質を持ちます。これは正孔と呼ばれ有効質量はｍ_ｈと表します。

この見かけの量子である正孔は電子に対する反物質の陽電子に似ています。しかし、ある有名な固体物理学の教科書では、このような正孔を陽電子という反粒子に対応しているように見えることは特に意識しないでよいと書かれています。実際、正孔は多数の電子の集まりの示す一つの姿ですから、そう書かれるのも無理はないのですが、筆者はあまりそこまでいうこともないだろうと思っています。

むしろ、固体という多面性に富んだ対象を個別的に扱いそれぞれの物性に注目するのではなく、実際の固体は表面で囲まれた空間ですが、原子や分子の電子から見れば巨大な空間で、電子や正孔、励起子などが自由に飛び回れる空間だとみて、彼らの運動や変化に主な注意を向けると、それはそれで興味深い世界が新たに展開されるように思います。ここではそのような考えに立って話を進めます。

さて、Dは価電子帯の一個の電子が一個フォトンを吸収して伝導体へ移された場合で、電子は赤丸のエネルギーを持ちます。

このように、価電子帯の電子がフォトンを吸収して伝導帯へ遷移すると、一対の電子と正孔ができますが、お互い逆の電荷を持っているために互いが引き合って結合し、励起子という新しい量子が一個できます。

価電子帯の正孔の有効質量ｍ_ｈは、伝導体の電子の有効質量ｍ_eより一般には大きい（重い）の場合が多いので、電子と陽電子の質量が等しいくて二重星のような運動をするポジトロニウムと違って、励起子は水素原子のように正孔の周りを電子が運動するような形になります。

水素原子の電子のエネルギーは次の式で表されます。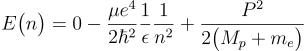
仔細は省略しますが、ここで右辺第三項は水素原子の運動エネルギーで、Pは水素原子の運動量、M_ｐは陽子の質量、ｍ_e は電子の質量、 µは換算質量と呼ばれる量でで表されます。

陽子の質量は電子のおよそ２０００倍も大きいのでµ～ｍ_eです。なお、εは真空の誘電率で、ここで使ってきたCGSガウス系では１です。この式の右辺の第一項の０は、止まっている原子の電子のイオン化エネルギーをゼロと決めたからです。

なお、主量子数ｎの電子の拡がりの半径ｒは、ボーア半径をa_０（～０．０５ｎｍ）とすると、となります。ｎ＝１００の電子では半径は５０0ｎｍに達します。因みに新型コロナウイルスの半径は５０nm程度といわれています。

一方、ワニエ励起子のエネルギーは次の式で表されます。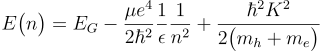
ここで、Kは励起子の波数です。

右辺第一項、E_Gは伝導帯と価電子帯のエネルギー差（バンドギャップ）です。後で紹介する半導体では、上の図のようにバンドギャップがｋ＝０にあります。このような場合は直接ギャップ半導体と呼ばれます。

第二項のµは、正孔と電子の有効質量の差は水素原子ほど大きくはないものの物質によって値は違います。このためエキゾチック原子の科学という立場からすると、ポジトロニウムに比べて励起子にはいろいろな種類があるという興味があります。

εは結晶の誘電率で正孔と電子との距離や物質によって違います。その理由は電子の広がり方に応じて正孔から受ける力が、他の沢山の電子の影響を受けて弱くなるためです。つまり、電子と正孔に働く引力が、電子同士の反発力で多少打ち消されるわけで、励起子の半径、r_exciton、は、水素原子に比べて主に誘電率εの効果でおよそ一桁大きくなります。　亜酸化銅結晶の励起子ではｎ＝２５まで観測されています。

補遺：励起子の波動関数ψ_exは、伝導帯の電子の波動関数、φ_ｃ、価電子帯の正孔の波動関数、φ_ｖ、及び電子と正孔の相対運動の波動関数,φ_relを掛け合わしたものとして　となります。ただし、波数がKの励起子といっても、電子と正孔の組み合わせは多数あるので、それらをすべて重ね合わせたものが実際の励起子の波動関数になります。

なお、電子や正孔はスピンをもっているために、励起子もそれを反映した性質を持っています。これはポジトロニウムと同じ事情ですが、専門的になるのでここでは触れないことにします。