５－a 補足

一個の電子による電気分極の振動を表すニュートンの運動方程式は次の式で表されます。
ここでｍは電子の質量、eは電荷です。なお、ここでは簡単のために摩擦の効果は無視しています。
今　のように振動するとすると、ｒは次のように表されます。
この式の両辺にeを掛ければ、分極を次のように表すことができます。
このような分極の集団が一体となって周波数ωで同じ位相で振動すると考えると、物質全体としてのマクロな分極はミクロな分極の密度をρとして、次のように表されます。　なお、pはベクトルですから、向きがバラバラではPは生まれません。
これから、電気変位Dが次のように得られます。これはεEとも表現でき、εはその物質の誘電率で、屈折率の二乗とも表現できます。

マックスウェル方程式によれば、 なので、次の関係式が得られます。
従って、この関係式を満たす解は、ε＝０つまり、と、があることがわかります。
前者は横波を表し、εがゼロですので、を考慮して、屈折率ｎについて次の関係式が得られます。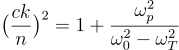

ここで、　と決めています。一方後者のを満たす波は、波の進む方向ｋとＥが並行ですから縦波になります。この波の周波数は　から求まりますが、ですので、とできます。