５　励起子ポラリトン

励起子は、一対の電子と正孔がポジトロニウムのように結合した量子で、絶縁体や半導体の結晶の中の多数の電子が電磁場と相互作用した結果生まれます。励起子が関係する光学過程を扱うときには、まず多数の電子の電子状態をシュレーディンガー方程式の解として求め、その最低のエネルギー状態（基底状態と呼ばれます）の電子が電磁場と相互作用してできるとして、時間を含んだシュレーディンガー方程式を解くという手順を踏みます。しかし、そうではなく、最初から励起子という量子があるとして、それとフォトンを一つの体系とした量子状態として励起子ポラリトンという新しい量子を求め、それを基に光学過程を説明する立場もあります。ここでは塩化銅の結晶で、そのモデルがふさわしい筆者のかかわった実験結果を紹介します。

ポラリトンの概念は最初ウクライナのトルピゴ（Kirill Borisovich Tolpygo 1916 – 1994),が、格子振動の量子のフォノン（横波の振動量子）とフォトンのまじりあった量子を予言し１９４９年に論文で発表しました。

１９５７年には、同じくウクライナのペカール（Solomon Isaakovich Pekar　1917 – 1985) がその概念を励起子へ発展させ、light-excitonと呼びました。その翌年、ポーランド系アメリカ人のホップフィールド（John Joseph Hopfield (1933-) がこの概念を世に広め,ポラリトンと呼び、今日この名前が使われています。筆者がこの概念を初めて知ったのは１９６６年に京都で開かれた半導体物理の国際会議でのHopfieldの講演でした。ちょうど壇上で時間係をしていたところで、おもしろくて夢中にノートをとっていると「時間係に専念せよ」と後で会場係りに叱られました。以来励起子ポラリトンは筆者の頭の中にいつも生き続けていましたが、実際にそれを実感したのはずいぶん後のことです。因みにこのホップフィールドは１９８２年に現在ホップフィールド・マシーンと呼ばれるニューラル・ネットワークの基礎理論を拓いた人でもあります。

（ずっと後年、理化学研究所でのある国際集会で、彼と廊下で話をしたことがあり、下で紹介する私たちの論文の別刷りを手渡したことがあります。彼は目を細めてなるほどと図を眺め、もう一部の別刷りにニコニコしながらサインをしてくださいました。なるほど柔らかい感じで、生き物の不思議に目を向けている方だと思いました。

彼は今年（２０２４年度）のノーベル物理学賞を授与されました。励起子ポラリトンの概念で半導体の光の分散現象を微視的に理解することから、単純な物理学のモデルよりかなりかけ離れているかに見える脳のネットワークへと彼の思考が発展するのは筆者には自然に思え、彼の受賞を嬉しく思いました。

もう一人の受賞者のヒルトン氏は「AI界のゴットファーザー」と呼ばれる方だそうです。彼はAIの危険性を警告してグーグルを退社した方だそうですが、それならその対策にはその後どのように貢献されたのでしょう。ちょっと原爆の開発した方々の戦後の発言を思い出しました）

さて、励起子ポラリトンとは、どんなものなのでしょう？

ここは量子論でどうというよりは、電荷がついたバネが外部の電磁波で強制的に揺り動かされ、ある条件で共鳴するとどうなるかを、光の屈折率のミクロなモデルとして古典力学でまず考えるのが分かりやすいと思います。これは一般の力学では強制振動といわれる現象で、この振動の振幅が非常に大きくなると、大きな橋がちょっとした風で大きく揺れて突然崩落したり、低周波の地震波で高層ビルが倒壊したりする危険な現象も起きます。

透明な物質の屈折率ｎは、物質の中の電子が音叉のようにあるきまった周波数ω_０で振動するバネのようなものであると考え、そのバネの集団が光の電場に揺すられて全体が位相を合せて（コヒーレントに）振動すると考えることによって理論的に説明することができます。

このモデルはローレンツモデルと呼ばれ、数学的な扱いは４４－aに示しますが、ここでは結果だけを絵で示します。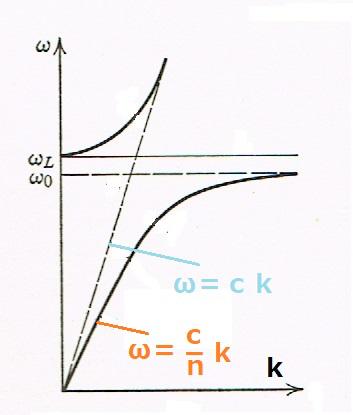この絵は物質中に誘起される分極の周波数を、波数ｋの関数として描いたものです。ω_０とω_Lはそれぞれバネの固有周波数と縦波の周波数、太い曲線は波数の関数として得られる横波の周波数ω_Tです。
ω_Tとｋの関係と、縦波の周波数は次の数式で表されます。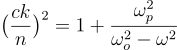

、ここでω²_ｐはと決めた量です。また、ρは電子の密度で原子の気体では原子の密度に比例します。これは以前には光と電子系との相互作用の大きさを表す量で、表参道を走るタレントの人気度を表す量のようだとその節では例えました。

ω_０もω_Lも波数ｋには関係しませんので、図では水平の直線や破線で示しています。ここで斜めの破線は真空中の光を表し、傾きが光速ｃです。ω＜ω０の（透明な）領域では、太い曲線は概ね直線を思え、傾きはｃを屈折率で割った値になり、物質中の光の位相速度を表しています。

光の周波数がω_０に近づくに従って、曲線の傾きは緩く（屈折率が大きく）なり、ω＝ω_０では無限大になります。実際にはバネの摩擦（この場合は分極と電場の位相のずれ）の効果（これが物質による光吸収になります）によって、無限大にはなりません。それはブランコの振れに逆らってまずいタイミングで押すと振れが止まるのと同じです。また、電子の密度が高いと真空の光の直線と曲線の開きが大きくなることは、ｎが大きくなるということで、これまでにも述べてきた事情を別の角度から示したことになります。

さて、ω_０が多数の電子の励起状態である励起子のエネルギー（塩化銅の１ｓ励起子のエネルギーが例としてふさわしい）に対応させることができます。この場合はω_０は波数の関数になりますので絵のようになります。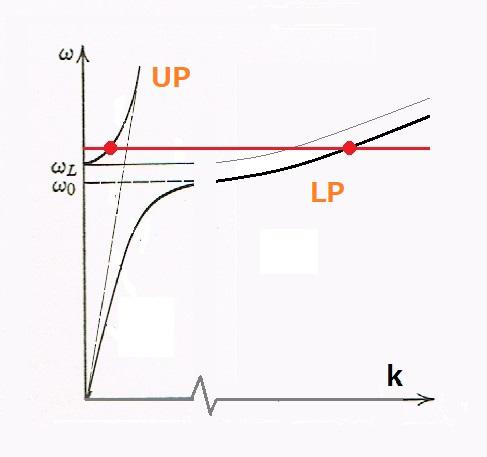

このように光と電子が相互作用した結果として、励起子ポラリトンのエネルギーが太い曲線で描いた二つの波に分かれるのですが、それぞれ励起子のUP (Upper Polariton)とLP (Lower Polariton)と呼ばれています。ｋ＝０では、ω_０とω_Ｌは一致します。この絵ではその差は波数によらないで一定としてますが、本当は波数が大きくなると小さくなります。ここで重要なことはω＞ω_L（ｋ＝０）では、同じエネルギーをもったLPとLUが共存することです。このため外部から結晶に入ってきた光は表面でこの二つの波に変換されるわけです。しかしのの二種類のポラリトンは結晶中での伝わり方や速さが違ったり、格子振動から受ける影響が違ったりしますので、励起子だけを考えるのとは違った励起子ポラリトンでこそ分かりやすく説明のできる現象が現れます。しかし、表面でこの二種類のポラリトンへどのような確率で入射したフォトンが変化するかは、よく分からないので、長らくの研究のテーマになっていて、何か余分の条件を決める規則があるのではないかと考えられていました。これは余分の境界条件、英語でAdditional Boundaru Conditionと呼んで、略してABC問題といわれてきました。

さて、ω_０≪ωの領域を見ますと、エネルギーは波数に比例しているように見えますので、ポラリトンはほとんどフォトンの性質を持っていることになります。しかし、、ω～ω０付近では励起子の性質を色濃く持つようになります。つまり、フォトンの領域ではLPの波数に対する勾配が物質中の光の屈折率を表しますので、屈折率の起源が励起子によることがわかります。一般に不純物の少ない透明な結晶では、このような性質を示すものが多く、ωがω_０に近くなると光の吸収が透明から突然不透明になるように見え、そこはそれぞれの物質が固有に示すスペクトルの特徴として基礎吸収端と呼ばれます。

というわけで、励起子ポラリトンは結晶の光の屈折率を量子力学で解釈するためのモデルにも見えますが、実はもっと光学過程を考えるときに重要な意味を持ちます。これを実際に筆者が実感したのは、筆者が東北大学のグループに就職して、後で紹介する励起子分子という量子を研究するようになってからでした。その事情は後で励起子分子の紹介のときに説明します。

その後もっと励起子ポラリトンを筆者が実感することがありました。励起子のエネルギーに光がちょうど共鳴するような波長領域（ω_０の付近）は非常に光の吸収が大きくて、測定が難しいはずなのに、UPとLPが直接波として干渉する様子が鮮やかに測定できる例を目の前で見せてもらったのです。それは東北大学からMitaが筆者のグループにスタッフとして加わったときでした。ある日彼から「こんな実験は（いまさら）意味があるだろうか？」と驚くべきデータを披露してもらったときです。彼は東北大学で塩化銅の励起子分子についての当時の段階としては最先端の研究を博士論文にまとめましたが、このデータはその趣旨から少し外れていたので温めておいたもののようでした。筆者はその鮮やかなデータに本当に驚き、ぜひ研究を続けるように勧めました。そうしてその後発表された論文のスペクトルが次の図です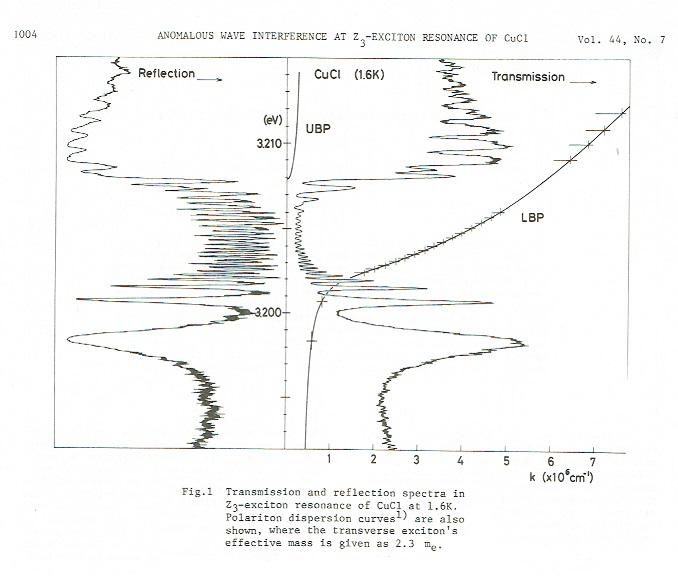

塩化銅のZ₃励起子の共鳴する全領域にわたって明瞭な干渉縞が光の透過と反射スペクトルに記録されています。この結晶の板の厚さは０．１５ミクロンという薄さで、とても筆者が自分で扱うことはできないようなものでした。測定温度は絶対温度１．６度（摂氏－２7０度より少し低い）という超流動状態のヘリウムの液体に浸けての測定です。不器用にやれば大体途中で結晶が割れ、吹っ飛んでしまう危険があります。凄いなあ、よくこんなデータが記録できたものだと目を丸くしたのを憶えています。

彼が尋ねた訳は、似たような興味から別の物質の結晶で行われたロシアのグループの論文が以前に知られていたからです。でも、塩化銅でやり直す価値は十二分にあると筆者確信しました。

この図には先に述べたUPとLPのエネルギーを波数の関数として描いた曲線が重ねて描かれています。ω＜ω０では、結晶を透過した光と一度結晶の裏面で反射して再び透過した光が干渉した干渉縞が見えています。しかし、ω＞ω0では干渉縞のピッチがちょうど半分で、UPとLPが結晶内部の反射とは関係なく直接干渉したものであることが分かりました。このデータではUPとLPが干渉するパターンが見えていますので、このABC問題を吟味するには好都合であることがわかります。なお、ABC問題はかなり専門的になりますので、ここではこれ以上触れません。

とにかく、このデータを基礎にいろいろな理論的な発展がありました。中でもChoらによる詳しい理論解析と、関連する電磁気学の基礎にもかかわる光学応答の理論が発展するきっかけの一つにこのデータが役に立ったことは幸いでした。また、関連する興味深い実験もみつかりましたが、それについては４４－ｂで補足します。

現在ではポラリトンの概念は大きな結晶の励起子だけでなく、人工的にデザインされた物質などへも使われ、広く電子系と電磁場を合わせた量子として、いろいろな物質での光学現象の解釈に使われています。

なお、Mitaはその後かねてからの考えで有機農業を生業とすることにし、以来着実に事業を展開していましたが、福島第一原子力発電所の事故で発生した放射線を帯びたプルーンで農場が汚染され非常に迷惑を受けました。しかし、彼は地元の人々の不安を解消し、汚染度の正しい評価のためのボランティア活動を立ち上げ、持ち前の物理学の知識を十分活用して地域の社会に貢献し、今も継続中です。特に世間ではあまり知らされる機会が少ない、ホットパーティクルという、事故時にコンクリートなどがガラス化した微粒子（ナノ粒子）に閉じ込められた放射性物質が一個あたりとしては非常に高い線量をだす微粒子を採取し、あまり注目されないβ線による内部被ばくの危険性を、非常に地道で精度の高い計測によって指摘しています。励起子ポラリトンについての上の測定結果とともに記憶されるべき成果だと筆者は思っています。