9 共鳴蛍光
投稿日 : 2021.12.18
M. Goeppert が二光子過程の理論で博士論文を取得したのと同じころ、同じM.ボルンの学生だったV.Weisskopfは、原子の自然発光過程による励起準位のエネルギー幅(有限寿命による不確定関係から現れるエネルギーのぼやけ)を指導者のE. Wignerと共に考察し、博士論文を書きました。
Barry R. Mastersの“The Origins of Maria Göppert’s Dissertation on Two-Photon Quantum Transitions at Göttingen’s Institutes of Physics 1920-1933”
(Shaul Katzir, Christoph Lehner and Jürgen Renn (eds.): Traditions and Transformations in the History of Quantum Physics : Third International Conference on the History of Quantum Physics, Berlin, June 28 – July 2, 2010に掲載)
によれば、2人はディラックの理論に強く影響されてそれぞれの学位論文をまとめたそうです。
Weisskopfの理論は、原子の電子励起状態が光と相互作用して基底状態へ遷移するときの発光スペクトル幅に関するもので、Weisskopf-Wigner Theoryと呼ばれています。この理論はHeitler とS.T.Maによって深められHeitlerの教科書(邦訳:輻射の量子論)にその概要が述べられています。この理論の結果だけを次の図によって示します。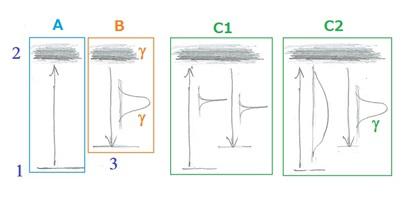
原子の電子の基底状態を1、励起状態を2、3は1と同じまたはそれに近い2より十分低いエネルギーの電子状態とします。
Aは基底状態1から励起状態2へフォトンを1個吸収して、電子が励起される過程を表します。
Bは励起状態2にある電子が自然にフォトンを一個放出して状態3(1でもよい)へ遷移する状態を表します。
Bの過程が起きる原因は真空の揺らぎと電子との相互作用によります。これは前に述べたn+1の1の効果で、アインシュタインのB係数として効率が得られるものです。
励起状態は一般には不安定で有限の寿命を持ち、不確定関係によってエネルギーには一定のぼやけが生まれ、そのぼやけはスペクトルの線幅として観測されます。その大きさの目安がγです。ですから寿命が短いほどγは拡がります。
C1とC2はHeitlerらの理論による光学過程を示します。彼等の理論の概要は次のようなものです。
外部の電磁場によって電子状態1の電子と相互作用する時、入射光のスペクトル幅がγより十分に狭い(単色性がよい)場合には、入射フォトンは状態2を中間状態として、すぐに状態3(または1)へ遷移します。これは光学過程としては、励起状態2の電子がフォトンの吸収し、再び放出するという2種類の光学過程が続いて起きるというのではなく、フォトンが状態2に共鳴する光散乱でありラマン過程です。方違いの話です。
一方、入射光のスペクトル幅がγに比べて十分広い場合には同じような散乱が起きるのですが、その場合の散乱光のスペクトル幅はγとなります。つまりBの過程が起きたようにみえるのですが、実は入射光と散乱光の位相関係が定まっている(コヒーレント)になります。そのため彼らは、これを共鳴蛍光と呼んで、自然放出による発光とは区別すべきだと考えました。
この理論を励起子分子の光学過程と比べることは、原子と多電子系の一形態の励起子では、γが決まる要素の仔細が違うために簡単にはできないのですが、それを承知の上で比べてみました。そのために一台の装置で2種類の波長とスペクトル幅を独自に変えられるように改良を加えました。その結果の一例が右の図です。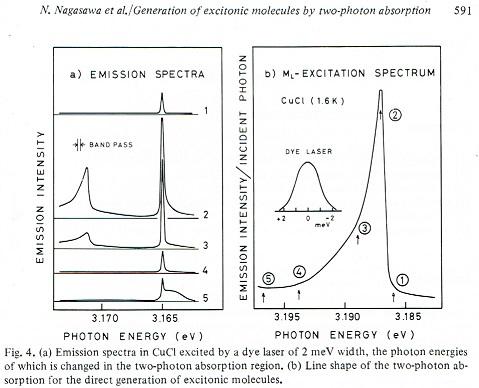
入射光のエネルギー幅を0.42meV程度では、励起子分子を二光子共鳴させることによって二光子ラマン散乱が観測されました。しかし、入射光のスペクトル幅を2meVに拡げると、1~5まで入射光のフォトンエネルギーを変化させても観測される鋭い発光線のエネルギーは変化しないことが左側の図からわかります。右側は鋭い発光線の励起スペクトルです。①、②などで励起した時の発光線が、左のスペクトルにある1,2,などに対応しています。
もしこれを上の理論で説明できるとすれば、励起子分子のエネルギー幅γは0.42meVと2meVの間にあるかように思えます。しかし発光線の幅は、それよりずっと狭いので、理論との直接の比較は出来ないことがわかります。
この問題については、Mitaが非常に周到な実験を繰り返しました。しかし、結局、幅の広い入射光の際に現れる鋭い発光線の起源は主に二光子ラマン散乱ですが、全てであるという確証はその時点では得られず、二光子共鳴で励起子分子ができないとはいえませんでした。
それからおよそ2年後、Grunのグループで、二光子共鳴ラマン線の測定がなされ、そのときに、筆者らが測定したのと同じ、入射光の波長に依存しない鋭い発光線も観測し、N線と呼んで、冷たい励起子分子からの発光だとしました。(Phach1978)(Hoenerlage1978)。
(ある会合でGrunと歓談していたときのことです。彼は筆者に、「Nってあなたの名前の意味ではないよ。Newの意味だよ」といたずらっぽくウインクしました。こちらは引き合いに出されて光栄だといってお互い笑ったものでした)
その後、試料の温度がおよそ30Kより低いと励起子分子と音響フォノンによる散乱は顕著でないことが報告されました(Itoh、1980)。
一方、1990年には、励起子分子のエネルギー幅の波数依存性が測られ、K~107cm-1でも高々150μeV程度であることが分かりました。(Kuwata-Gonokami1990)。
更に、1994年には波数K=3×103cm-1程度の励起子分子では、およそ30µeVであることが測定されました(Hasuo1994)。
このように励起子分子のエネルギーのぼけは非常に小さく、吸収スペクトルの幅などで測られすスペクトルの拡がりは、主にコヒーレントな散乱効率のスペクトルを反映した不均一幅と思われました。
ここでToyozawaのコメントで始まった共鳴散乱の話題が盛り上がったころ、気になりながら具体的なイメージが描けなかった話があります。それはR.Kubo(1920-1995)が、いわゆる磁気共鳴の分野ではよく知られたモーショナル・ナローイングという現象ではないかという指摘です。この現象は、オランダと米国籍のN.ブレンベルゲン(Nicolaas Bloembergen、1920-2017)が1948年の学位論文で明らかにしたものです。
これは例えば核磁気共鳴において、不均一な局所磁場の効果が核スピンの運動に対する大きなランダムな揺らぎの原因となっている時に、統計学の基本法則の中心極限定理によって、不均一な揺らぎに比べて平均的な揺らぎの方が少ないことが実測されるという現象です。この現象は気体や液体の原子や分子では、それらが静止しているのではなく動いているので、その瞬間的な揺らぎの効果より、時間平均した揺らぎの方が少なく見え、それが狭いスペクトルとして観測されます。
Kuboらの共鳴ラマン散乱スペクトルに対する論文によれば、比較的単純なモデル(Huber 1970)による計算によって、この効果が原理的には光学スペクトルにも表れることになります。この現象が励起子分子状態が2光子共鳴散乱の中間状態となっている場合にも起きているのではないかという説でした。
M発光スペクトルの解析から想像されているように、極低温(大抵の実験は4K以下が多いが)に冷却した塩化銅の結晶の励起子分子系が、いろいろな実験条件にもかかわらずいつでも絶対温度Tで20から30Kで熱平衡になっていると見えます。この場合の熱浴は励起子系が担っていると想像されてきました。つまり励起子分子系は常に励起子との衝突によってエネルギーを交換していると考えられてきました。このように考えると、励起子分子から見れば励起子との相互作用は時間的に激しく揺らいでいるので、時間的に不均一な力が及ぼされていると考えることができます。ところがどちらも動いているので、(波数の大きい)速く動く励起子分子は波数の小さい遅いものよりある時間内に多くの励起子と遭遇してエネルギーが大きく揺らぐ、その結果、波数のゼロの励起子分子のエネルギーの揺らぎが統計的な平均に近く見えて、波数ゼロの励起子分子によるスペクトルが鋭く見えるのではないかというわけです。
この話については、その頃、箱根でこの問題についての小さな研究会があったとき、湯上りで涼みながらKuboの話を直接聴く機会が偶然ありました。しかし、なにせ統計力学の基本的な理解が不十分な筆者には、その時に励起子分子の光学過程との関係に応用してどう理解できるかを訊く力が不足していて、上のような解釈の是非について彼のコメントを得るまで行かなかったのはとても残念でした。その後、別の機会に、もう少し具体的にしたモデルを彼から直接聴く機会がありました。そして筆者はあろうことか「その内できるだけ理論と比較できるような実験を必ずしてみます」と約束してしまったのです。しかし、結局できずじまいになってしまいました。
何時だったでしょうか、旧知のフランクフルトの理論家H.Haugは、ある会合でこんな言葉で講演を締めくくったことがあります。
”All theory is wrong, but it's a matter of degree. All experiment is right, but a question is what they measure"
というわけで、励起子分子が2光子励起で実際に出来ていることは否定できません。励起子分子と励起子の多重の弾性散乱によって、リアルに粒子が励起されるといえるのでしょうか?
この問題にもう一度直考える機会が、それから相当後にでてきました。1991年の秋、L.V.Keldyshの弟子の故A.L.Ivanovというロシアの若い理論家が、励起子同士の相互作用による光学非線形応答という理論を発表しました。当時KeldyshはHaugと共同研究をしていた関係で、彼も加わっていたのですが筆者それを知りませんでした。
翌年、ウイーンでの会合である不可解な出来事に出会いました。Hanamuraの講演が終わった後で、一人の若者(これがIvanovでしたが)が立ち上がって、猛然とコメントをしました(まじめな彼の癖で食って掛かったように聞こえるのです)、しかし、対する講演者の意見はどうも明確でなく、どうして? と少々不穏な空気が会場に流れて終わりました。講演の後で、「どうしたの」とHaugに尋ねると、かくかくしかじかと訳を教えてくれました。そして、Ivanovを紹介してくれました。このような雰囲気は、その後も何度も場所を変えてあったようですが、筆者にはその理由はいまでも良く分かりません。
物理の要点は、Hanamuraの励起子分子の2光子吸収の理論は、M. Goeppertの場合のような扱いですが、Ivanovらの見解では、この光学過程がすべて励起子ポラリトン間の相互作用で説明でき、高次の相互作用をすべて繰り込めるというもので、その違いが二光子吸収スペクトルの形に現れるので、どちらが妥当かを実験で確かめられるというものでした。その意味で励起子分子はBi-Polaritonと呼ぶのが妥当だというものでした。
彼らの考えは筆者には自然でしたし、これを実験で確かめるのは興味深く、さっそく準備に入りましたが、装置の改良やなにやら、理論家とは違って実験サイドは「はい、すぐ」とはいきません。資金も必要です。この実験はHasuoが中心になって、可能な限り精密な結果を求めて実験を進めました。長くなるので省略しますが、その結果、彼らの考えが少なくとも塩化銅の励起子系では妥当であるとの結論をかなりの精度で得ました。
この研究では、Ivanov、Haug、Keldishなどと筆者の研究室で親しく話す機会がありました。Ivanovはモスクワにいる親思いの若者で、寒い冬のために秋葉原で電子ジャーを買って親のためにプレゼントしたり、研究上ではなかなか戦闘的でしたが日常はとても誠実な人柄でした。その後、彼はイギリスのカーデフの大学に就職しました。一度研究室を訪れたことがありましたが、フィッシュ・アンド・チップスをいつも好んで注文していました。それからかなり経って、突然彼の訃報を耳にしました。何があったのか筆者は不案内ですが、誠実で信頼できる理論家を失ったことは非常に残念です。
コメント