９　アインシュタインは手品師か？

真空中で光は毎秒およそ３０万ｋｍ進みます。これがこの宇宙での制限速度です。正しくは、２９９７９２．４５８ｋｍ/secです。小数点以下どれほどの数字が並んでいるのかは分かりませんが、とにかくこれまで行われた実験では、これを超える速度は観測されたことはありません。

この宇宙では、この最高速度を超えてスピード違反はできないのです。この数を小文字のｃと書いて「光速」と呼び、物理学の基本になる決まった数（定数）一つです。

どうして制限速度があるのでしょう？　筆者はこのようなきりの悪い数になる本当の理由を知りませんが、とにかくこの制限速度があるのは厳然とした実験事実です。

この数値になる理由ではなく、この実験事実を説明するための理論が（特殊）相対性理論です。

１９０５年にアインシュタインがこの理論を論文で発表したとき、世界中の人々は仰天しました。今まで慣れ親しんでいた時間や空間の概念がぶち壊されたのです。そして、４次元の世界という絵に描けない空間を論じる、わけのわからない難解な凡人には絶対に理解できない理論というような話が強調されたので、大騒ぎになりました。でも、基本となる考え方は誰でも知っている次の現象が基礎になっています。

電車が一定の速さVで右へ動いています。Aさんは駅のプラットに立ち止まって、電車に乗っているBさんが手を振っているのを見て手を振っています。

このときAさんから見るとBさんは電車と一緒に速さVで遠ざかっています。しかし、Bさんから見ればAさんは逆に左へ同じ速さで遠ざかっています。しかし、実際に起きていることはAさんとBさんの距離が離れていっているだけです。このように一つのことが起きているだけなのに、見る場所で運動が違って見えるわけです。つまり、見え方はどこから見るかによって相対的に違って見える。この現象を筋道だって考えようというわけです。

そこで、このような見かけの現象をどのような数式で表し、これからどうして制限速度が説明できるのかを次に示します。

W.パウリがまだ学生だった時に、A.ゾンマーフェルトの勧めで書いた、"Theory of Relativity"という有名な書物があります。その最初に相対論の歴史とともに、基本的なことが短く見事にまとめてあります。また、次にはこの理論を扱う「数学の道具」という節があり、ここでおなじみのピタゴラスの定理の成り立たない４次元の世界の扱いの基本がまとめられています。

相対論の教科書などは、この「道具」を基礎にしていますので、かなり高級な数学の訓練が要ります。しかし、アインシュタイン自身も初めからこの手法に通じていたわけではなく、後で数学者から習ったといわれています。

物理学を習ってもすべての人が職業としての物理学者になるわけではないし、まして、社会に出てから仕事や教養としてこの理論に興味を持った人々に対して、この「道具」をつかって解説がされても、ほとんどこけ脅しとか、煙に巻く道具のようになり、これがこの理論が、アインシュタインの名前と共に神聖化してしまったのではないかと思います。

さて、止まっているAさんのいる世界（Ｋ系とよく言われます）とAさんに対して一定の速度Vで動いているBさんのいる世界（Ｋ’系）では時間が違っていると、１８８７年に論文で発表したW.Voigt（和文もありますが、英文の方が詳しく紹介されています）という学者がいます。その後、ローレンツは１８９２年に同様な考えを発表しましたが、Voigtのことは知らなかったそうです。やがて、１９０４年に、また翌年、ローレンツとポアンカレが、Ｋ系とＫ’系での位置と時間の関係を次のような数式で表現しました。

、

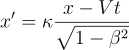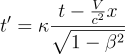
ここで´のついた量はK'系の量を表します。κはある定数でその意味はよく分かってなかったそうです。ここで、βは次の数を表します。　なお、ｃは真空中の光速です。Voigtは　と考えていたそうです。

アインシュタインはκが１であることを明らかにしました。つまり、次の関係式を導いたのです。これは今日、ローレンツ変換と呼ばれます。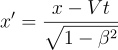

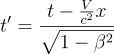
高校生の読者は、これらの式をｘ＝、ｔ＝の式に書き換えてみると面白いことがわかります。しかし、この式を初めて見て瞬時に答えのわかった方は、アインシュタインと同じレベルの羨ましい感性の持ち主だと思います。

　さて、いかがでしょう？

実は計算するまでもなく、ｘ'→ｘ、ｔ’→ｔと置き換え、ＶをーＶにすれば終わりです。上で述べたＡさんとＢさんの関係で違っているのはＶの向きだけでした。ですからＶの符号を替えればいいわけです。アインシュタインは、まずこの常識的な現象を表すにはκ＝１でなければならないことを見つけたのです。

この関係から、動いている人の時計は遅れ（だから長生きするとか言われたり）、物の長さが縮む（ローレンツの収縮、Vが大きくなると進む方向だけ物体がぺちゃんこになるように見える）など、怪奇現象が起きるというので、大騒ぎになったわけです。アインシュタインは手品師のような存在です。このような一見変なことが見える原因については、こちらで種を明かします。

さて、最高速度制限の話に移りましょう。

ローレンツ変換の公式からＫとＫ’系での速度の次のような関係式は得られます。

上の話ではＡさんもＢさんも止まっていましたが、ＢさんがＶと同じ方向に速度ｖ’で歩いている（動く歩道を想像してください）として、それをＡさんが見たときのＢさんの速度ｖとｖ’の関係を表した関係式です。ここで、この速度はＶではないことに注意してください。ここでは小文字のｖを使います。

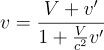
もし、Ｖ＝０なら、ｖとｖ’は同じです。この公式の出し方もこちらに示しました。

ここでｃに比べてＶがずっと遅いとき（普通の場合はそうです）には、分母のＶ/ｃ^_２の部分はほとんどゼロですので分母は１となりますから、Ｂさんの速度はＶだけ増えてAさんには見えます。これは私たちが普段知っていることです。

ところが、もしＢさんが光速ｃで歩く（これは実際ロケットに乗っても無理です）としますと、ｖはやはりｃのままになります。これはちょっと計算すると分かります。ですから、ｃより速いものはない。つまりこのような理論で制限速度があることが説明できることが分かります。

素粒子の実験に使われる加速器では、電子や陽子が光速に近い速さで運動します。そのような物体の運動を考えるときには、相対論を必ず考えないとわけがわからなくなります。また、GPS用の人工衛星は、地球の自転による地上の移動速度より速く地球のはるか上空をまわっていますので、相当速度は速くなります。そのため地上より衛星の中の時間が相対性原理によって遅れます。したがって、これを補正しなければGPSで現在位置をただしく求めることができません。本当はこれだけでは不足で、後で述べる一般相対論による地球の重力の強さの違いによる時間のずれも補正する必要があります。この効果は地上の方が重力が強いので遅れます。

注：ローレンツ（Hendrik Anton Lorentz、1853-1928）はオランダの物理学者です。ローレンツ変換がアインシュタイン変換と呼ばれないのは、どれだけこの人の貢献が相対論の発見に大きな影響を与えたかを示しています。

ポアンカレ（Jules-Henri Poincare,1854-1912）はフランスの数学者、理論物理学者だけでなく、広い分野で重要な業績を残しました。特に電磁場と相対性原理との関係の基礎は彼によるといえます。しかし、彼の相対論への貢献は、アインシュタインの陰に隠された気配があります。

アインシュタイン（Albert Einstein,1879-1955）は、いうまでもなく現在の物理学の基本的な理解に必要なほとんどすべてに大きな貢献をした物理学者です。彼の特徴は、色々な先人の知識を一般人の感覚を生かせて発展させ、速やかにエレガントな理論にまとめあげる稀有な能力に恵まれ、更にエンターテイナーの条件をよく心得ていた人でもあったように見えます。