１０　原子力って、どんな力？

「原子力」という言葉はだれでもご存知ですね。でも、そんな力はありません。

この「力」は、原子の持っている「能力」というような曖昧な意味で、原子に起きる変化の余りとして出てくるエネルギーのことを表しています。

このエネルギーを表す数式が、E=mc^２であることも有名です。

この関係式はアインシュタインの関係式と呼ばれ、これほど社会的に深刻な影響を持ち続けている物理学の数式はないのではないかと思うほどです。原子爆弾はこのエネルギーを火薬の代わりに使ったものですし、原子力発電では、このエネルギーを使って巨大な「やかん」で湯を沸かし、その湯気の力で発電機を回します。どちらも人類にとっては麻薬のようなもので、中毒症から抜け出すにはかなりの意志力がいるやっかいな代物になっています。

この関係式が特殊相対性理論から導かれることをご存知ですか？

ここではアインシュタインの論文を基に、その原理を紹介します。彼は１９０５年の論文で、止まっている電子が電磁場から力を受けて速度ｖにまで加速されるまでに、電磁場が電子に与えるエネルギー（専門用語では仕事といいます）Wを計算して、そこでｍｃ^２がエネルギーであることを示しました。ただしｖはcに比べてずっと小さい場合を考えました

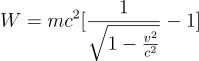
この関係式の求め方はこちらを参照してください。

ｖはｃよりずっと小さいですから、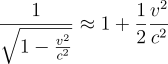とできますので、Wは次のように表されます。この式は、電磁場から得たエネルギーが、そっくり電子の運動エネルギーになったことを表しています。この式の括弧の中の１－１を０としないで残しておいて書き直すと、次のようになります。

ここで、もし電磁場がなかったとしますと、もちろん何も起きませんからｗもｖもゼロです。そうすると、ｍｃ^２＝ｍｃ^２となります。それがどうした？というところですが、この関係式はとても重要な意味があるのです。つまり、電子が動いていようが、止まっていようが電子にはいつもｍｃ^２というエネルギーが備わっていることを暗示しているのです。このエネルギーをE₀としますと、つぎのように表現できます。

このようにｍｃ^２が質量をもつものが備えているエネルギーであることがわかりますが、実はこれはアインシュタインの式として知られている次の関係式とは違います。

数式の形は似ていますが、意味は同じではありません。その理由はすこし専門的になりますので、余談に回しました。

こうしてｍｃ^２が特殊相対論から導かれるわけです。