１１　重力で光が曲がる

宇宙空間はほとんど真空なので、光が曲がって進むことなどなさそうに思えます。しかし、太陽のような質量の大きな星の周辺では太陽の重力の効果で光は曲がって進みます。この可能性は特殊相対論から５年ほど後の１９１５年に発表された、アインシュタインの論文によって予見されました。彼の重力についての理論は、今日一般相対論と呼ばれています。

その3年後の1919年5月29日、南大西洋で皆既日食が見られるので、イギリスの天文学者、エディントン（Sir Arthur Stanley Eddington、1882-1944）らは、この機会をとらえてアインシュタインの予想を確かめるために観測チームを組織し、太陽の近傍に見える恒星の位置を観測しました。そして、アインシュタインの予見を実証したとする論文を発表したのです。

特殊相対性理論によって、物の長さが縮んだり時計が遅れたりするというので人々が驚いたことに加えて、今度は重力で光が曲がることが実証されたというので、アインシュタインの名声は一気に高まり、一躍時代の寵児となり、ベルリンの社交界の人気者になりました。そして、巷では人々はなんでもかんでも「相対性、相対性」と大騒ぎになったそうです。

では、この理論はどのような経緯で生まれ、どのような理論なのかを考えてみます。

マックスウェルがフックの考え方に沿って電磁場のポテンシャルを媒介として、真空に近い宇宙空間でも電荷や電流の間に力が働き、その力の伝搬はｃを超えず、相対論と矛盾しないことがわかりました。

アインシュタインは、その考え方が万有引力にも使えないかと考えました。

というのはニュートンの万有引力の考えでは、質量と質量の間に働く力は、何かに媒介されるものではなく瞬間的に直接作用すると考えますので、例えば何光年も離れている質量の間に働く重力では、光の速さｃよりはるかに速く伝わらなければならなくなり、特殊相対論に反するわけです。

そこで、彼は真空といえども質量を取り囲む空間には、その質量の大きさに応じた「ゆがみ」が発生し、それを相手の質量が感じたものが万有引力だと考えました。そしてそのゆがみの伝わる速度はｃを超えなくてもいいことを説明しました。その理論が１９１５年のアインシュタインの論文で発表されたものです。

専門的な解悦書や教科書では、この理論は、前に述べたパウリのいう４次元空間を扱う「数学の道具」を基礎に説明がされますので、それを理解するにはその道具に精通する必要が出てきます。しかし、そもそものこの理論の考え方は、ごく日常で私たちが経験する現象をどう筋道だって理解できるかということで、専門家だけに分かるものではなく、誰もが知っていておもしろい話だと思います。

私たちがエレバーターに乗って降り始めたときに、一瞬フワッと浮き上がる感覚があります。危険な話ですが、もしエレベーターを吊っているロープが切れてそのまま長い距離を落下し続けたとしますと、中の人は無重力を経験するはずです。しかし、それを外から見ると、その人はエレベーターの箱と一緒に重力によって落下します。このように見る場所によって重力があったりなかったりするのはなぜだろう？　彼はエレベーターではなく、「屋根から飛び降りた人が重力を感じなくなるのはなぜか」と考えたのだそうです。

ここでは理論は後にして、光が重力によって曲がって進む理由を直観的に考えてみます。

次の絵の左側は、部屋が重力で落下しているものです。壁のAにレーザーがあって、反対の壁の同じ高さにあるBを水平に照らしています。これを見た部屋の中の人は、光はまっすぐに進んでいることがわかります。

さて、右の絵はこれを部屋の外で止まっている人が見るとどう見えるかを示したものです。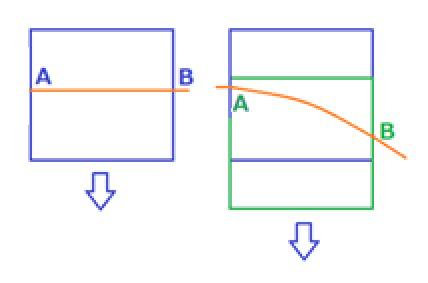レーザーの光はBに届くまでにすこし時間がかかります。その間にも部屋は落下しますので、Bの位置は外から見ていると下へ移動しています。（例えとして緑で示しています）しかし、光がBへ向かうことには変わりはないので、結局外から見るとAを出た光が曲がってBへ届いたように見えるのです。

このように、一つのことが起きているのに、見る場所によって光がまっすぐ進んだり、曲がって見えたりする。つまり見方によって違ったことが起きているように見え、この場合はその原因が重力による加速度運動であることがわかります。アインシュタインの理論は、見る場所によって相対的に違って見える運動を筋道だって理解しようというものです。

エディントンらが観測したような現象を、グリセリン入りのゼリーで見ることができます。透明な容器の中に円筒を置いて、周りにゼリーを流し込んで固めます。ゼリーが固まったところで円筒を引き抜くと跡に穴が開きますが、そこへ１００％のグリセリンを流し込みます。すると、グリセリンがゼリーの中へ浸み込んで穴の周りではグリセリンの密度が外側に向かって緩やかに低くなり、それに伴って屈折率も小さくなります。次の図は、重力で太陽の周りの空間が歪んでいる様子の想像図で、皆既日食起きた太陽の周りはこんな感じなのでしょう。

下の図はレーザーの光を穴の側面に向って通したところです。細い線で描いた円の位置に穴があり、この穴を太陽の代用品とみると、レーザーの光は穴の外側で曲がって進んでいるのがわかります。

赤色の直線は遠くの星の光が重力によって曲がらずにまっすぐ進んだとしたときの道筋ですが、実際は緑の線に沿って進みます。これを離れた場所から見ると、まるで緑の直線を上の方へ延長した先に星があるように見えるわけです。

このように大きな質量の星の周りがレンズの働きをする現象は重力レンズと呼ばれ、この宇宙で数多く発見されています。最近は大きな質量を持った星やブラックホールが強い重力源であることが分かってきましたので、宇宙空間の未知の重力源とされる暗黒物質の分布図もこの現象利用して作られているそうです。

次の図は、先ほどのゼリーの後ろに赤いＬＥＤランプを置いて上から見た様子で、黒い丸は質量の大きな天体の代用品です。ＬＥＤの位置を移動させるとレンズの周りに見える光のパターンが変わり、ちょうど真後ろになるとリングが見えます。宇宙空間で見えるこのようなリングは「アインシュタイン・リング」と呼ばれています。
アインシュタインは時間的に変化しない電荷ρ（正しくは電荷密度）の周りにできる静電ポテンシャルφが、という方程式の解として表される電磁気学の理論を、重力を生むポテンシャルΦにも応用して、という方程式の解として求める方法を見つけました。

そして質量（密度μ）があることによって、その周りで、位置に時間を加えた４次元の空間が、質量のない空間に対して変形するとして、この変形を万有引力係数Gの４次元空間の幾何学的性質と結び付けて数式化しました。

これがアインシュタイン方程式という一般相対論の基礎方程式です。この方程式を理解するには、多次元の幾何学についての知識や数式の扱いがパウリのいう「数学の道具」です。しかし、アインシュタイン方程式そのものの説明は、ここでの範囲を超えますので、以下では、その結果として得られる三つの話題について紹介します。

１）時間の進み方が重力によって変化します。この効果によって、人工衛星の高度と地上での重力の違いが時間差を生むので、これを補正しなければGPSは実用化できません。また、この事実が私たちが身近に感じられるこの理論の検証となっています。

２）重力源となる質量（太陽、地球、ブラックホールなど）がある時空での物体の運動は、４次元空間でのフェルマーの原理によって予想できます。特に重力が弱く、光速に比べてずっと遅く運動する物体が、ニュートンの運動方程式に従うことが、この理論から導かれます。これから物体の動きやすさを表す慣性質量と、物体の感じる重力の大きさを表す重力質量が同じであることが分かり、これがガリレオ・ガリレイの実験の原理になります。

３番目はブラックホールの存在ですが、これについては後の節に譲ります。