１２　時空のゆがみ

重力源によって４次元の時空がゆがむ様子を知るためには、パウリのいう「数学の道具」が少しいります。ただ、４次元空間といっても絵が描けないので、ここでは横軸としてｚ軸だけにして、縦軸をictという量を表す時間軸を考え、次のような絵を考えます。ここで、i は　i^２＝ー１となる数です。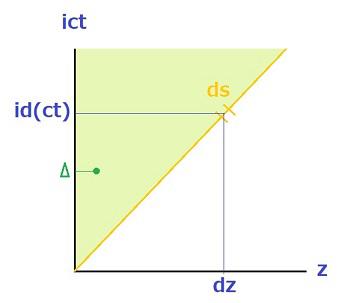

オレンジ色の直線は４５度傾いた直線で、その直線を細かく等分に分割した一片をｄｓとすると、ピタゴラスの定理から、と書けます。

真空中では、光の進む距離はですから、光はこのオレンジ色の直線に沿って進みます。

光以外の物体は草色（教科書などでは円錐状で示されています）で示した空間の中を運動します。Δはこの空間のある点での時間の刻み（瞬間）を表す量（局所時間、Local Timeと呼ばれます）です。

もし空間がゆがんでいると、ｚ軸と時間軸の刻みが変化します。そしてもしz軸の目盛りの間隔が大きくなると、物体の実際の長さは縮んで見えます。

また、時間の刻みが短くなると、実際の時の流れが遅く（なかなか時間が進まないように）見えます。

そのゆがみは次のように表すことができます。　ここでξとηは、その時空での縦軸と横軸の刻みの変化の程度を表し、重力源の大きさや、そこからの距離によって変わります。

１９１６年、シュワルツシルド（Karl Schwarzschid ,1873-1916）という天文学者が、天体が質量Ｍの完全な球形で回転もせず、電気も帯びてないとして、さらに重力場が方向に寄らず中心からの距離ｒだけで表されるという最も簡単な例について、アインシュタイン方程式の厳密な解を求めました。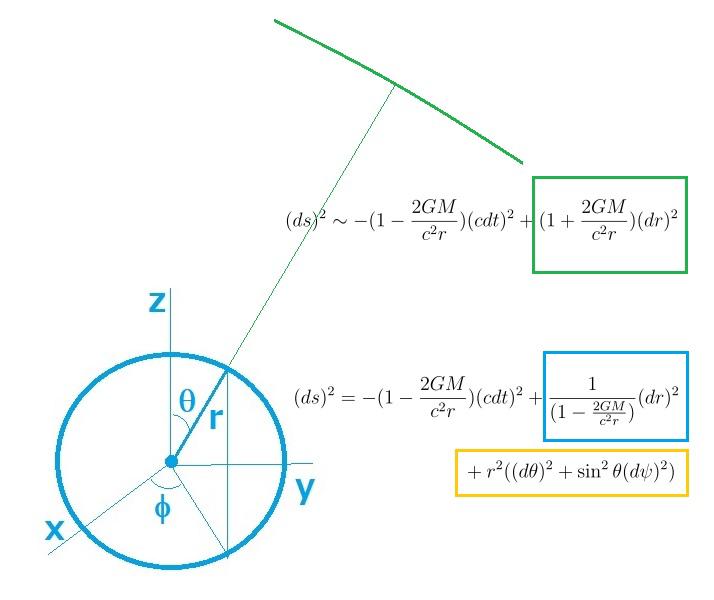この場合、(ds)²（metric：計量と呼ばれます）は、上の絵の下側の数式が彼の結果で、一般にこのような重力の働く時空は、重力源を中心として重力の強さは球状に拡がっていますので、極座標で表されています。ここでＧは万有引力定数です。

このメトリックをと比べると、ξとηは１ではないので、時空が歪んでいることがわかります。

重力源の中心から十分離れた場所に話を移しますと、その時は上の絵の上側の数式で表現できます。

この距離での重力は非常に弱いので、下の式の青の矩形で囲んだ部分は、上の式の緑の矩形で囲んだ部分のように近似できます。また、遠くでは重力場の拡がる球面はほとんど平面とできるので、下の式のオレンジの矩形で囲んだ角度に関係する微小量は無視できます。

結局、この場合は、、となっています。

ξの値は時間の歪みですから、地球の重力を考えると地上と人工衛星のいる高度ではｒが違う、歪の程度が違います。その効果によって人工衛星の時間と地上の時間が違ってくるわけです。したがって、特殊相対論による時間のずれに加えて、この効果を補正しなければ、GPSで正しく地上の場所を決められません。このように、GPSが実用に使えるようになったことが、特殊相対論と一般相対論の実証になっているわけです。