１３　フェルマーの原理

イカの目玉のレンズの中で光が曲がって進むことは、フェルマーの原理によって説明でき、次の数式で表せました。　これは屈折率ｎを道筋に沿ってAからBまで足し合わせた総和が最小になるように光は進むという原理でした。

また、光の屈折率ｎを質量ｍに置き換えると、同様な数学的処理（変分法）によって、その物体の運動の軌跡が計算できました。

重力源のある４次元の空間も、フェルマーの原理によって、その物体の運動を説明することができます。

ここでは、簡単のために空間はｚだけにして、弱い重力が働く時空のゆがみから、ニュートンの運動方程式が導かれ、ガリレオ・ガリレイの実証した事実を一般相対論から説明できることを説明します。

この場合のフェルマーの原理は次のように表現できます（ここでは始点Aと終点Bの表示は省略しました）。ここでｍは重力源にある質量Mの物体による時空のゆがみを感じている（重力を受けている）物体の質量です。ここで、ｄｓは次の関係式から得られます。

次の図は前節で示したものと同じです。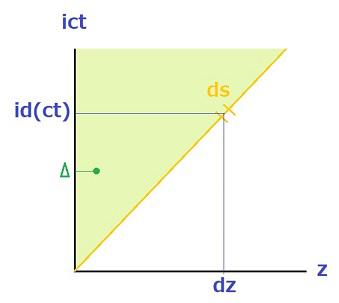

質量ｍの物体は黄色で示した領域（この図には縦軸、横軸の負の領域は省略しています）で運動します。今は、物体の速度がｃに比べてずっと小さい場合を考えていますので、オレンジ色の直線はほとんど縦軸のようなことになり、物体はほとんど縦軸に沿った領域を運動します。

つまり、ｄｓの長さは icdtとほとんど同じなので、ｄｓの替わりに時間の微小な変化量Δ（局所時間）を使うことができます。つまり、と考えます。

従って、道筋の長さが最小になるための条件は、次の式で表現できます。　

一方、重力ポテンシャルを、　　と表すと、フェルマーの原理はつぎのようにできます。

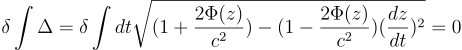
この数式で、ｔはこの運動を見ている人の時刻、は速度です。

ここで、補足で示すような数式の処理によって、を導くことができます。

この式にｍを掛けて見やすい形に整理しますと、次の方程式が得られます。 。

また、をｚで微分してこの方程式に代入しますと、結局

が得られます。これはニュートンの運動方程式で、右辺は万有引力ですが、地球上ではMが地球の質量、ｚを地球の半径としますと、右辺はーｍｇとなり、ｇが重力加速度です。したがって、地表の高低差や地球内部の構造や密度によってｇの値は違います。詳しい話はこちらにあります。

これから、慣性（力によって運動が変化する程度を表す）質量（慣性質量）と、重力を感じる程度を表す質量（重力質量）が同じであることが一般相対論によって説明できました。これがこの理論で得られた最大の成果といえます。

補足：上に示したファルマーの原理を表す積分のルートの中にある１以外の項は小さいので、近似計算をしますと、結局この積分は次のように書けます。　　ここで、として、オイラーの方程式：に代入して計算すると、が得られます。