１８　フォトンは「のっぺらぼう」

プランクによって光の強さはエネルギーではなく、フォトンの数であることがわかりました。でも、そのころの学者たちが「あたりまえだ」と思って気にしなかったフォトンのとてもたいせつな性質がありました。

フォトンの顔は「のっぺらぼう」でなくてはならなかったのです。「のっぺらぼう」って目も鼻も口もないお化けですよね。沢山いても、どれがどれだかわかりません、区別がつかない。

プランクの公式を導くには、フォトンが「のっぺらぼう」と考えることが絶対に必要なのですが、当時このことを意識的に気に留める学者はいなかったようです。

区別がつくかつかないかが、どれほど大きな違いかを、三連符を使って考えてみます。

一組の三連符は、三つの違った音の組み合わせでできています。ここでは例えとして、この一組が周波数νの電磁波を抽象的に表す同じ振動数の振り子（振動子と呼ばれます）に当てはめ、これに３個のフォトンが配分されている状態を表しているとします。

次の図は、赤「ド」、黄「ミ」、緑「ソ」の音を順番を取り換えてできる三連符を適当な順に１２個並べたものです。区別ができないフォトンだけがある場合を表すために「ド」だけの三連符も、一オクターブ下の音で示しました。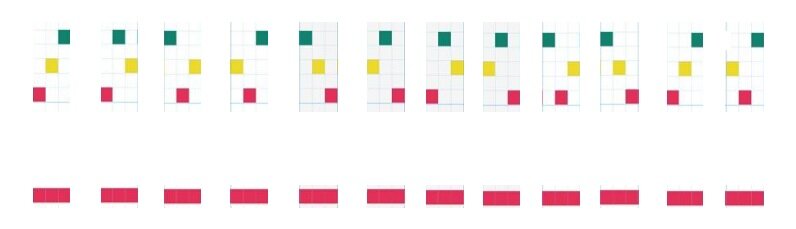

フォトンが区別のできるものなら、このように色々な種類の三連符による調べが現れ、その種類は三つの音の順序の違いから６種類あります。つまり、この例では特定の三連符が見つかる確率は六分の一です。

しかし、フォトンが区別のできないものと考える場合は、いつも同じ三連符が並びますので、同じ三連符が出る確率は１で、区別できる場合に比べて６倍多くなります。

フォトンがｎ個ある場合（ｎ連符ですが）でも同じで、ｎ個の音符が全部違う場合に比べて、全部同じ音のときには１ｘ２ｘ３ｘ・・・・＝ｎ！（ｎ！はｎの階乗を表す記号です）倍多くなります。

このようなフォトンの性質を次のように数式で表すことができます。今振動子にｎ個のフォトン分のエネルギーが溜まっていることが観測される確率を考え、区別できる場合を、区別できない場合をと表しますと、次の関係があることになります。

ここで、ある空間でフォトンが一個増えたと分かる確率を、区別できる場合を、区別できない場合をとします。

すると、一個増えたことが観測できる確率は、それぞれでとですから、

、また、についても同様に表されます。

一方。のことです。なお、と書けます。したがって次の関係式が得られます。

この関係式の意味は、何かの原因である空間でフォトンの数が１個増える確率は、フォトンが区別できない場合は、区別できる場合に比べてn+1倍多くなるということです。

たとえばある空間で原子が一個フォトンを放出するとしましょう。その時、その空間にすでに同じフォトンがｎ個観測できる状況では、その原子が同じフォトンを放出する確率はn+1倍高くなることになります。このフォトンの性質を利用した光源がレーザーです。

アインシュタインは１９１６年、原子がフォトンを放出する確率が2種類あり、その一つはｎに関係することを見つけました。上の関係式で言えば、（ｎ＋１）のｎの部分が誘導放出（Stimulated emission）と呼ばれる部分、また１の部分は自然放出（Spontaneous emission）と呼ばれる部分です。

彼は熱平衡にある原子の電磁波の吸収、放出についてのエネルギーバランスの統計的考察に基づいて、誘導放出過程の存在を発見しましたが、ここでの扱いでは、簡単な数学の組み合わせの規則を使って、両方の放出過程を同時に理解できるので、問題の本質を知るにはこの方が簡単で分かりやすいと思います。また、レーザーの種類はいろいろありますが、どのレーザーにもこの考えは使えます。

このようなフォトンが区別がつかないものだということを意識してプランクの放射公式を、１９１１年に理論的に導いた学者がいます。

この学者はポーランドの理論物理学者ナタンソン（Wladyslaw. Natanson, 1864-1937）で、「同じエネルギーのフォトンはどれも本質的に区別がつかないという性質を備えているものである」という、今日の物理学の用語では、「不可弁別性（indistinguishability）」と呼ばれる性質を初めて論文で示しました。しかし、この論文は、当時の有力な学者たちは知っていながらその重要性を見過ごしてしまいました。

１９２４年になって、インドのボース（Satyendra Nath Bose, 1894-1974）がスマートな理論を発見し、それにアインシュタインが大興奮、プランクの輻射公式に新しい発展を導きました。この理論は今日ボース・アインシュタイン統計と呼ばれます。

ナタンソンの論文がボースと同等の理論だったことは第二次世界大戦の後まで忘れられてしまいました。一方、ナタンソンと同じころ東北帝国大学の教授だった石原純もボースと同じ考えで論文に書きましたが、やはり、忘れられてしまいました。

この歴史については、このブログの『あるポーランドの学者の残照：L.ナタンソンの論文をめぐって』を参照ください。