２２　レーザーが育んだ知の伝承

ルビーを使ったレーザーが最初にでき、続いてHe-Neレーザーのような気体を使ったものが開発されました。これらは研究者たちが自分たちで組み立てたもので、それを使って研究できるのはその人たちですから、多くの先駆的な研究が生まれました。そもそもレーザーの理論や開発は欧米と旧ソビエトが中心でしたので、そこからこのような研究が生まれるのは自然で、そこで育まれた研究者たちがその後世界中に拡がりました。ここではその中心的な役割を果たしてきているある研究者たちを追ってみました。

レーザー光の特徴は、非常に強く、スペクトルも非常に狭く、今までに類のない光源でしたので、当然多くの研究者が先を争ってこの光を使った研究を始めました。ただ、一つ困ったことはレーザー光の波長が当時の装置では変えられないことでした。

そこで二つの流れが生まれました。一つは光の強さを利用して、元の振動数の２倍（波長が半分）の光を作ろうというものです。フルートでいえば、強く吹いて一オクターブ高い音を出すようなものです。こうして、現在ＳＨＧ（Second Hermonics Generation)など、非線形光学現象と呼ばれる現象が発見され、適当な結晶に強いレーザー光を透過させて元の光とは違った波長の光を作る方法が開発されました。例えば現在市販されている緑色のレーザーポインターは、 808 nm の半導体レーザーを使ってＹＡＧ（イットリウム・アルミニウム・ガーネット）結晶で発生する波長が1064 nm の赤外線のレーザー光を、KDP結晶（KH2PO4）に当て、そこで発生する波長が半分にあたる532nm（緑色）の光を使ったものです。

もう一つは、レーザー光の波長そのものを連続的に変えられる仕組みを考案して分光学に使おう、という流れでした。この目的のレーザーを可能にしたのは、窒素の気体を使った紫外線を出すレーザーの開発でした。これによって、適当な有機物の色素（たくわんを黄色くするようなものから猛毒のものまでいろいろあります）を適当な溶媒に溶かした液体が、紫外線を吸収して発する蛍光を使うものです。種類の違う色素分子の発光はそれぞれ固有の広い波長領域に拡がっていますので、色素を選べば必要な波長のレーザー光を取り出すことができます。その後、窒素レーザーではなくエキシマ―レーザーという、希ガスのイオンを使ったレーザーの紫外線が色素レーザーとセットで使われるようになりました。

１９７０年、ヘンシュ（Theodor Wolfgang Hänsch, 1941-）はスペクトルを非常に狭くできる色素レーザーを発表しました。次の絵は彼らが開発したレーザーの基本構造のスケッチです。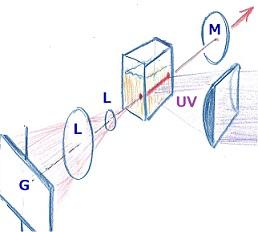かまぼこ型の凸レンズで窒素レーザーの紫外線を透明なセルにいれた色素溶液に絞り込んで当てます。すると赤い筋で描いた部分が光ります。この光の内、右側の鏡Mへ向かうものと、左にGとある回折格子に向かう光に注目すると、回折格子からは特別の波長の光だけが戻ってきますので、MとGの間でその波長の光だけが行き来し、セルの中で誘導放出が起きてレーザー光が生まれますので、これをMから一部取り出して使うわけです。回折格子は広い面積を使った方が行き来できる光のスペクトルを狭くできますので、彼の考案したレーザーでは、絵にLと示した二枚の凸レンズ、L（望遠鏡のようなものです）で光束を広げてスペクトルを狭くしました。その後、直角プリズムを２個使ってビームを広げる方法も考案されました。彼らはこの装置のGとLの間にファブリ・ペロ・エタロンという、光の干渉を利用したフィルターをさらに加え、0.004Aのスペクトル幅の光を作って精密な分光学を進め、水素原子を使って量子力学の基礎的な研究を行いました。この一連の業績に対して、2005年に彼はノーベル物理学賞が授与されました。このレーザー装置はヘンシュ型と呼ばれ、回折格子を回転させることによって、レーザーの光の波長を連続的に変えることができます。

ヘンシュと一緒に精密な原子分光学の研究をした学者に、弟子のワイマン（Carl Edwin Wieman 、1951-）がいます。彼は１９９５年に、エリック・コーネルと共にアインシュタインが１９２５年に理論的に予想してから初めてボーズ・アインシュタイン凝縮（BEC）を、⁸⁷Rb気体で実証しました。この成功はヘンシュから受け継がれた精密分光学のノウハウが見事に実を結んだ例となりました。その直後筆者はある財団からノーベル賞の候補者を募るアンケートを受け取りました。筆者はワイマン氏を推薦しました。当然多くの学者たちも彼を推薦したはずです。そうして彼はコーネル氏と共に２００１年にノーベル物理学賞を受けました。この研究については後でもう一度触れますので、ここではこれ以上述べません。

アインシュタインはプランク公式を数学的に説明したボースの理論を、理想気体（お互い相互作用しない質量のある希薄な気体）で、気体の粒子の数が定まった場合に拡張して、BECを理論的に予言しました。しかし、フォトンは物質によって吸収されるので数が定まらないために、フォトンの集団ではBECという現象は起きないと考えられ、すべての統計物理学の教科書にはそう書かれています。

しかし、２０１０年、フォトンの集団もBECを起こすという実験結果をヴァイツ（Martin Weitz）らが発表しました。彼もヘンシュの弟子で１９９２年に水素原子の高分解分光に関する研究で博士となり、その後チュウのグループで冷却原子の研究を行いました。そして、ヘンシュの開発した色素レーザーを彷彿とさせるような相対する二枚の鏡の隙間に、ローダミン６Gというありふれた色素の溶液の雫を表面張力で保ち、そのマイクロキャビティーの中の色素が吸収したり放出したりするフォトン集団でのBECを実証しました。筆者はこの研究を知った時、教科書とは違う状況を実験で実証した彼らのアイデアに感心しました。この実験の興味深いことは、BECを論じる前提となる、フォトン系を温度Tで熱平衡に保つ「熱浴」という抽象的な概念を、実際の物質として吟味できることです。それを次の絵をつかって説明します。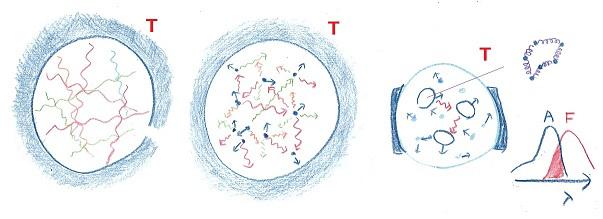

プランクの公式を導く教科書説明では、この絵の左端のモデルが使われます。まず魔法瓶のような内部が鏡のようなもの（空洞と呼ばれます）に、色々な波長の光が満ちているとします。この光は鏡を作っている物質が光を吸収や放出をした結果であり、魔法瓶（空洞の壁）は温度Ｔで一定であるとします。そこで空洞内にある特定の波長（振動数）の光に対して仮想的な沢山の振り子を当てはめ、その振り子の振れ（エネルギー、フォトンの数）が平均的にどのなっているかを計算します。しかし、これはプランク以後に考えられた洗練されたモデルで、実際の温度Tの物体が光を発する機構との関係はどうでもいいことになります。

この考え方は理論的には正しいのですが、今一つ現実味が薄いと筆者は思ったものです。ところが、このモデルをとらず、電磁気学だけから、プランクの理論以前に信じれていた放射公式（レーリー・ジーンズの公式と呼ばれます）を導く物質を重視したモデルがあります。この考えから現在の教科書のモデルが定まった理由がボルン（Max Born,1882-1970）による“Atomic Physics, （鈴木良治・金關義則訳『現代物理学』みすず書房）”に詳しく書かれています。光の放出や吸収の実態を重視した泥臭いモデルも、普通はフォトンの数は一定にはならないのでBECは起きないという理由を考える上で役に立ちます。

すなわち、このモデルでは、まず電荷が外力を受けて速度が変化した時、その電荷が毎秒あたり外部へ放出する電磁波の平均のエネルギー が計算します。その基本的な考え方は１８９７年に発表されたラ-モアの論文にあります。彼は電荷（イオンとしています）の出す放射率をその論文の５１２ページに次のような数式で表しました。"LXIIL On the Theory of the Magnetic Influence on Spectra ;and on the Radiation from moving Ions", J. Larmor, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science
Series 5Volume 44, 1897 - Issue 271 The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science Series 5 Volume 44, 1897 - Issue 271 (因みにラーモアはローレンツ変換をH.ローレンツと同じころに見つけた人です。また寺沢寛一はラーモアの弟子といえます）

一方、この電磁波は別の電荷に力を及ぼして仕事をしますが、その平均の仕事（エネルギー）も計算できますので、この両者がバランスして熱平衡に達していると考えます。この様子を光を吸収したり放出したりする主体が原子だとして示したものが、真ん中の絵です。

このモデルでは原子の気体は温度Tの容器とエネルギーをやり取りしています。熱は運動エネルギーの大きさの目安ですから、原子は容器の壁にぶつかって容器の内部の原子に力を与えたり、もらったりして、その平均的なエネルギーが温度Tで表されているわけです。各原子は色々な波長の光を出したり吸収したりしますが、どの振動数（波長）の電磁波の出し入れのエネルギーの収支もバランスしていると考えれば、温度Ｔの環境にある電磁波の平均エネルギーが計算でき、それが波長によらずＴに比例すると考えました。これがレーリー・ジーンズの公式です。

しかし、ある原子がある波長の光（絵の赤色の波で表しました）を放出して、これを別の原子が吸収したとき、その原子がその波長と同じ光を放出して、それを元の原子が吸収する割合は少なく、別の波長の光（絵では別の色の波で示しました）になったり消えてしまったりします。ですから特定のフォトンの数が原子の満ちているその空間で一定にはならないのがわかります。

この考えを拡張して、光のエネルギーをフォトンの数として換算し平均のエネルギーを計算したものがプランクの放射公式ですので、この公式を導く限りではフォトンの数が一定であるという条件は考える必要はなかったのです。したがって、フォトンの集団でBECは起こらないとされたわけです。ところがそうばかりとはいえなかったのです。

右端の絵はヴァイツらの考えを示したものです。彼らは向かい合わせの微小な鏡の間に色素溶液の雫をつけてマイクロキャビティ―としてその色素を光らせたのですが、彼らの使った色素の特徴として、吸収スペクトル（A）と蛍光スペクトル（F)がちょうど重なった部分があり、その特別な波長の光のフォトンについては、一個フォトン吸収した分子が再び同じフォトンを一個放出することが効率よく起きるので、キャビティーの中ではこの波長のフォトンの数はおおよそ一定になると考えたのです。また、色素分子は溶媒の分子と衝突してエネルギーを交換して熱的に平衡にあり、更に一個の分子は複数の原子がばねで繋がれているようなものなので、その振動エネルギーも熱的に周りと平衡になります。つまり、この空間では、その波長の光のフォトンについては、その色素集団が熱浴（魔法瓶の役割）として働くと考えられます。

そうすると、数が一定という条件が加わったので、ある条件ではBECが起きて良く、それだけでなく、溶液の温度や色素の濃度を自由に変えた実験ができるので、BECを調べることと関係して統計力学のもっと一般的な基礎研究も行えるわけです。実験の仔細は彼らの論文に詳しく述べられていますが、専門的過ぎるのでここでは省略します。筆者はこの種の研究から統計力学の基本的課題であるエルゴート仮説や、エントロピーの増大の法則の本質などがさらに深められるのではと感じています。

このような、基本的な基礎研究の連鎖から、色素レーザーの開発やその動機となった原子の精密分光学で培われた経験が、技術や知識ではなく、思想としての「知」として、世代を超えて伝承されていると感じました。これは二番煎じの拡散とは違います。