２７　狙いは的中、大成功

シュレーディンガーは、自分が導いた波動方程式でミクロな世界の現実を説明できるかどうかを、水素原子の電子の運動に当てはめて確かめました。つまり、水素原子の一個の電子が、原子核の中心にある陽子によって作られているポテンシャルに捕まっているときの電子のエネルギーを次の方程式によって解いてみたわけです。　

ここでｒは電子の芯からの距離、また電子の電荷を－eとしています。（実際の水素原子では、電子と陽子からできているので、陽子と電子の相対運動と、原子の重心の運動とに分けて計算されます）なお、∇^２は を表す記号です。

この波動方程式の解の性質は、すでにダランベール（Jean Le Rond d'Alembert、1717-1783）の楽器で生まれる音から始まった理論や、オイラー（Leonhard Euler, 1707-1783）、ベルヌーイ（Daniel Bernoulli, 1700-1782）、ラグランジェ（Joseph-Louis Lagrange, 1736-1813）などによる数学的な研究からよく調べられてきました。

（これらの学者たちの生い立ちを読むと、彼らがそれぞれに過酷な時代に生きていた様子が伺えます。なかでもラグランジュはマリー・アントワネットの数学教師だったとあり、どんな経験をしただろうと想像します）

シュレーディンガーは彼らの研究を基礎に、波動関数についての数学的な性質を、この方程式の解を求めるときに使いました。

具体的な方法は、どの量子力学の教科書や参考文献にでていることでもあるので省略しますが、その結果得られたエネルギーは次の式で表されることがわかりました。

　ここで、nは　１，２，３，・・・という整数です。このエネルギーがどれほど水素原子の電子のエネルギーを再現しているかということです。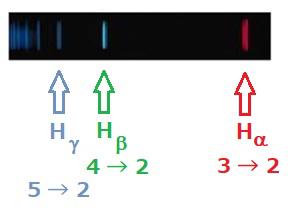

バルマー（Johan Jakob Balmer,1825-1898）は、水素原子の発光スペクトル線の間隔について、ある法則を１８８５年に発見しました。

更に、リュードベリ（Johannes Rydberg,1854-1919）は、それぞれの線スペクトル線の波長が次のような数式で表されることを１８９０年に発見しました。　ここでRは今日リュードベリ定数と呼ばれます。なお、ｍはｎより大きな整数です。

すこし飛躍しますが、図の例えば３→２などの意味は、シュレーディンガーの計算結果をもとに、ｎ＝３のエネルギーをもった電子が、フォトン一個を放出してｎ＝２のエネルギーになったことによる発光スペクトル線でることがわかり、分光学では水素原子のHα線と呼ばれます。上の図のスペクトル写真は、多数の水素原子が個々に出した光をある時間積算して記録したものです。

１９０８年、リッツ(Walther Heinrich Wilhelm Ritz ,1878-1909) によってすべての原子のスペクトルについてこの数式が成り立つことが明らかになりました。

（リッツは病弱で３１歳で亡くなりますが、アインシュタインとチューリヒのETHで同期の学者で、略歴を読むと非常に鋭い感性の持ち主だったことが分かります。彼の見つけた関係式が良く知られている割には、彼自身の研究の歩みは知られていないようです。彼の自宅は故郷のシオンに今も残っているそうですが、墓はブルドーザーで破壊されて今はなくなっているということです）

こうして、シュレーディンガーは、自分の理論で予想した電子の持つエネルギーの間隔から、実際のスペクトル線のエネルギーを定量的に説明することに見事成功しました。

彼の狙いは大当たりで、水素原子のようなクーロン引力のポテンシャルだけでなく、別のポテンシャルにも、この方程式が使える見通しがたちました。

実際、彼はフックの法則による復元力のポテンシャルによって振動数νで振動する微小な振り子（実際には分子の中の複数の原子核の距離が振動する（分子振動）についても彼の理論を使って、振動子のエネルギーが次の式で示されることを、論文では結果だけを示しています。　ここでnは０，１，２，３、・・・という整数です。

このように、シュレーディンガー方程式は、今では原子はもとより複雑な分子の電子や、電子が多数ある場合、分子の骨格の振動、一般に量子間の散乱現象なども含めて、ミクロの世界の運動を説明する基礎方程式となりました。

プランクは電磁場を架空の振動子と表現して、ｈνがその振動のエネルギー量子としましたが、上に示した振動子をその架空の振動子に当てはめると、振動数νの光のフォトン一個分のエネルギーがｈνになります。

ところが、上の振動のエネルギーの式のカッコの中には１/2となっていて、エネルギーの単位がｈνなのに、その半分のエネルギーなんて意味があるのでしょうか？

このエネルギーはゼロ点エネルギーと呼ばれ、量子力学の不確定性原理によると考えられています。実際これが影響を及ぼす自然現象がいろいろ実証されています。目に見える例としては、ヘリウムが決して固体にならないことがあります。

電磁場（光）の場合は真空の揺らぎとも呼ばれ、原子のスペクトルや、電子そのものの質量や電荷といった量に本質的に影響していると考えられています。しかし、この場合は振り子のようなイメージでは、うまく説明ができません。例えば、フォトンの位置などといわれても困ります。

この点についての話は別にするとして、今は先に進むことにします。