２８　ψとは？

シュレーディンガーは水素原子の電子の運動を表す自分の考案した方程式を解いて、実際に観測される発光スペクトル線の間隔を理論的に得られた電子のエネルギーから再現することに成功しました。

この計算は波動関数が一般にもっている数学的性質を利用して行われたのですが、弦や管の振動などが得られる波動方程式の解とは違って、確かに電子の運動をかかわっているのは明らかなのですが、ψの物理的意味についてははっきりしていませんでした。

現在標準的に受け入れられているψの解釈は、ボルン（Max Born, 1882-1970）によって提案されたもので、ψは確率振幅と呼ばれる複素数で表される波です。これは光の干渉のような性質を表すのに便利ですが、それ自身は測定できません。そして、実際に測定できる確率は実数ですから、その大きさは複素数の性質から、ψ^＊ψで表現します。ここでψ＊は共役複素数という数です。なお、複素数の性質はこちらにあります。

ψの性質を直観的に考えるために水素原子をモデルに絵に描いてみました。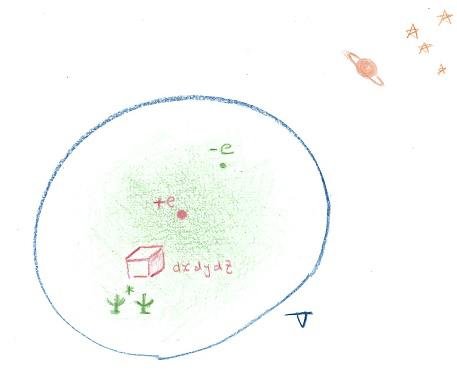

中心の＋電荷に引かれて電子は、シュレーディンガーが計算して得られたどれかのエネルギーを保って運動しています

標準的な量子力学の解釈としては、その内のどれかの波動関数をΨとすると、その電子がある体積Vの空間の中のｄｘｄｙｄｚという微小な体積の中で見つかる確率密度がψ^＊ψだと考えます。そして電子はVの中のどこかで観測できますが、外部で観測されることはないと考えます。

しかし、問題はＶの範囲をどのように決めるかです。

空間に境界はありませんから宇宙の果てまでとしても悪くはありません。しかし、そんなところで観測される確率は常識的にはほとんどないだろうと、その辺は人間がVの範囲を勝手に決めて、測定結果が大体再現されれば良しとしようという約束です。

シュレーディンガー方程式に限らず、微分方程式は初期条件とか、境界条件とか呼ばれる条件を最初に決めなければ解けませんが、物理学ではその点は、適当に条件を決めて結果オーライ、とおおらかというか、実利的といえます。絵で緑のボヤ―っとした部分が原子の芯のあたりで濃いのは、その辺で電子が見つかる確率が多いという意味で、何か雲のような実態があることを表現したものではありません。

Ψが量子力学でいう波動関数であるための約束事があります。すこし専門的すぎますが、興味があればこちらを参照してください、

ボルンはこの解釈などを含めて、この分野に貢献した業績によって１９５４年のノーベル物理学賞を授与されました。彼は２０世紀の前半の理論物理学に大きく貢献したハイゼンベルグ（Werner Karl Heisenberg, 1901-1976）やジョーダン（Ernst Pascual Jordan、1902-1980）、パウリなど多くの若い学者たちを、ドイツのゲッティンゲンで指導してきた人です。その時の受賞の講義録が公表されていますが、そこで彼がどのようにこの解釈をすることになったかについての、すこし曲がりくねった経緯が述べられています。この事情もこちらの後半に紹介しました。