３０　光学過程と方違い

２７節では、シュレーディンガーは水素原子の発光スペクトルが、量子数ｎの違う電子のエネルギーの変化として説明したことに触れました。ここではそのような現象を量子力学で扱う方法について考えてみましょう。

次の絵は電子がiというエネルギー状態から別のｆという状態へ、フォトンを一個吸収したり（左側）、放出（発光）したり（右側）する光学過程を描いています。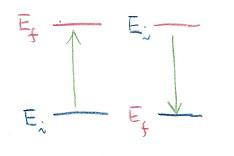

横棒は電子の時間的に変化しない状態（定常状態と呼ばれます）のエネルギーの位置（準位と呼ばれます）で、上にあるほどエネルギーが高いことを表します。ここでE _i やE_ｆは_、次のシュレーディンガー方程式で得られる電子のエネルギー、E_ｊ（ｊ＝１～ｎ）の内の二つです。

水素原子の電子を例では、V_e-pは電子と陽子の間に働く引力のポテンシャルです。この図は、最初　i　の状態（始状態、initial state、と呼ばれます）にあった電子が、光と相互作用の結果最終的にｆの状態（終状態、final state、と呼ばれます）を持つような光学過程の内、もっとも単純なものを表しています。

このような光学過程では、電子は時間によって電磁場（光）とのエネルギーのやり取りを扱うために、次の時間を含んだシュレーディンガー方程式と呼ばれる方程式を解いて考える必要があります。

ここで、V’は電子と電磁場との相互作用で時間的に変化します。ですから方程式の解の波動関数ψも時間によって変化します。そして、最初あるエネルギー状態に電子があった確率が時間的に変化して、別のエネルギーを持つ確率が加わってくると考え、その変化の割合で光学現象を説明しようというわけです。

具体的な方法はこちらにメモしました。

次の絵は、もうすこし複雑な光学過程の例です。

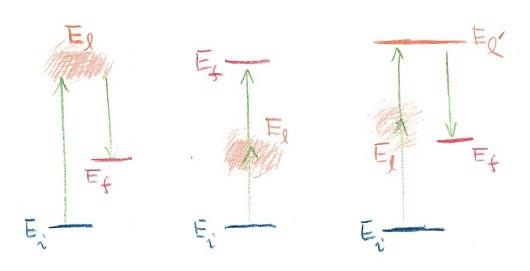
左の過程は二つの過程が引き続いて起きるもので、始状態の電子が光と相互作用してｌへ一旦遷移し、さらにｌからもう一度光と相互作用して最後に終状態ｆへ落ち着くという過程です。ここでｌという状態は中間状態と呼ばれます。

平安時代や室町時代には、ある目的地へ出発する日の方角が悪いと、その日の方角のよい方向にあるお寺などへいったん向かって宿泊し、そこから日を改めていい日に本来の目的地へ向かう「方違い」という習わしがありました。この習わしは、原子や分子の電子が、上のような光学過程を考える例えとして便利です。中間状態は一時泊まるお寺みたいな感じです。

実際の方違いでは、彼らは結構長くお寺に滞在したらしいのですが、光学過程では本当にそのお寺に泊まる必要はなく、泊ったつもりぐらいの非常に短い滞在時間だと考えられています。実は、一か所のお寺である必要はなく、同時に無数のお寺に寄ったつもり（実際は不明）でもOKなのです。

真ん中に示した光学過程は２光子過程と呼ばれるもので、この場合もどのような中間状態ｌを経由しているかは必ずしも明らかではありません。又、絵の右端の例は、さらに複雑なものですが、中間状態の中の特定のｌ’では、お寺の門をくぐってしまったような場合になり、電子は一泊することも、泊まらずにでていくこともできて、どっち付かずの状態が実際に起きます。このような状況で生まれる発光は共鳴蛍光と呼ばれ、最初の図で示した発光とはスペクトルの様子が違います。

シュレーディンガーは、最初の論文では具体的には示していなかったのですが、ボーアのいう光学遷移のミクロな光学過程を、以上のように彼の方程式から計算できることを彼はすでに見込んでいたわけです。

このようにシュレーディンガー方程式から色々なミクロな現象をが明らかにできるのですが、彼自身も波動関数というものを使えることの真意には納得できず、ボルンやボーアの主張する波動関数の確率的解釈には懐疑的でした。何故でしょう？　これがここでの次の課題です。