３３ー１　神様とのコラボ：量子暗号（Quantum Cryptography)

ベルのアイデアやアスペらの実験(1982)で、量子力学が必要になるミクロな世界では、半分生きて半分死んでいるという私たちには非現実に見える「変な猫」がいることがわかりました。

これまでのところ、ミクロな世界の自然現象は例外なく量子力学によって説明できてきましたので、アスペの実験を知ったとき、「やっぱりな」と筆者は安心してしまいました。ところが、そんな単純な筆者とは違って、さっそくこの「変な猫」に目を付けた頭の柔らかい人々がいました。その中には「量子力学で効率の良い計算ができるのじゃない？」と考えた（１９８５）ファインマンもいます。そして、実際に通信に使おうと、ベネット(Charles Henry Bennett , 1943 - )とブラザード（Gilles Brassard、1955-）による1984年に提案されたBB84と呼ばれる量子通信用のプロトコル（通信情報のやり取りの仕方についての約束事、つまり合言葉：パス・ワードの規則）や、エカート(Artur Konrad Ekert 1961-) によって１９９１年に考案された、EPRパラドックスやベルの理論を現実に活用したプロトコル、E９１などが生まれました。

どうして彼らは「変な猫」に目を付けたのでしょう？

その方面の研究者や技術者たちは、「絶対に第三者に漏れないパスワードをどう作るか」また、「秘密が漏洩したことをできるだけ速く感知して被害を最小限にとどめるか」を目標に、理論や技術を改良してきましたし、その技術が色々なところで使われてきているのでしょう。しかし、彼らは一つ基本的な不安を感じていたそうです。というのは、彼らの考案した最強と思われてきた暗号ですら、絶対安全だということが数学的に証明できなかったのです。

それで仕方なく、「パスワードを解読するためには、とても面倒で時間がかかる仕掛けを作っておけば、まあ実用上はいいだろうだろう」と、「面倒くささ」だけを暗号の有効性のよりどころとしてきたのです。ところが、コンピュータの処理速度がどんどん速くなって、どんなに手間のかかることも短時間であっさり処理できるようになってきそうなので、「やがて、時が来れば、頼るものがなくなってくるぞ。今のうちに何とかしないと・・・」という危機感があったのでしょう。事実、今ではパスワードが盗まれて大金が盗み取られるトラブルが起きています。ですから、その時に、「オイ、なんとかしろよ！」といわれるのは必至で、それから「前向きに検討いたします」では間に合いません。当時すでに現在の状況を予見していたのですから、流石です。そこに、アスペの実験で量子力学に基本的な欠陥がないことが検証され、しかもその固有な特性を検証できる数学的根拠も明らかになったというのですから、彼らにとっては量子力学が願ってもない助けの神様に映ったはずです。あのサイコロを振る神様に。そもそも神様に反逆してできたのが科学ですが、こんどは科学が神様とのコラボ？を始めるという皮肉で興味深い話になってきたともいえます。

アスペの実験室を訪れたころ、そんな心配なんて筆者にとってはほとんど他人事でした。当時スマホでお金の決済ができる時代が来るなんて少なくとも筆者には想像もできませんでしたし、「暗号」といわれても、せいぜいスパイの暗躍するする情報機関の象徴で、００７の映画を思い浮かべる程度のことだったのですから。

彼らは、「変な猫」でもねずみをとるならいい猫だ！　この猫使えるぞ！　と考えました。どうしてかって？　彼らは「変な猫」の持つ次の特性に注目し、その大きな可能性を直感したのです。

「変な猫」は、生きたの猫と死んだ猫の波動関数の和(重ね合わせ）です。（どうしてかはすぐ後で述べます）

EPRの思考実験のように、この状態である「変な猫」のいる部屋をどこまでも広く拡げても、理想的にはその巨大な部屋のどこにでも「変な猫」はいるものだ、という量子力学に問題はなくなりました。しかも、その部屋のどこかで誰かがそっと覗いて、「生きた猫」がいる、と知った瞬間、もうこの巨大な部屋のどこにも、つまり、覗いた場所からどんなに離れた場所でも「死んだ猫」は絶対見つからない。　

なんだって、どこにもいたはずの「変な猫」が消えちゃう！　ということは、覗かれたことが遠方に伝わるってことか！　宇宙の果てまでだって・・・？　これだ！　という訳だったのです。

でも、どのようにこの「変な猫」を飼いならして、絶対安全なパスワードを作ったり、それを使った情報の安全な伝達ができるのでしょう？

このアイデアが生まれてからすでに３０年以上経っています。１０年ひと昔といいますが、そうなると、もう大昔のことです。その間にこの分野の進歩はとても速く深くなっているようで、ちょっと関連論文の数を調べて見ると分かりますが、その数はもう大変なものです。ですから最先端の状況までを筆者が理解することは到底できません。そこでここでは、これまでベルのアイデアや、EPRのパラドックスを話題をしてきたついでに、こんな話もあるということで、この「変な猫」の飼い方の原理のあらましだけを、エカートの考えなどや、実際に実験でテストし、銀行の通信に試したという、この方面のタレントの一人であるツァイリンガーの２００８年のある論文を参考にして考えてみることにしました。また、この拙文を書いている間に筆者が感じたことも付け加えています。ですから、全体として３３は「余談」ともいえそうです。

さて、これまで特に意識的には触れてこなかったのですが、量子暗号や関連する量子力学の応用にとって最も基礎となる波動関数の性質を、光の干渉を示す有名なヤングの二重スリットの実験によって念のために振り返っておきます。量子力学の波動関数や「変な猫」について、この実験はよく引き合いに出され、どこにでも解説があるものですので、今更と思われるかもしれませんが、「変な猫」のプロフィールの紹介のつもりです。この実験の仕組みは図のようなものでした。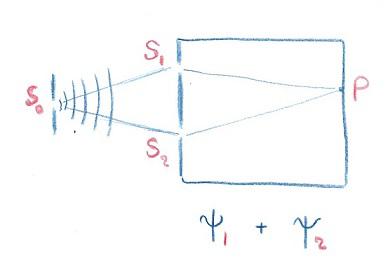

二重スリットといいながら、S_０，S_１、S₂と３個スリットがあります。S_１とS₂はS_０から同じ距離にあります。スリットとは狭い隙間ですが、簡単のためにここでは針の先で開けたような小さな穴としましょう。

ご存知のように、二つのスリットの先にある壁に干渉パターンができます。でも、何時でもはっきりと見えるとは限りません。

S_０は何のためにあるのでしょう？　

ここで、以前に紹介したホイヘンスの原理を振り返ります。S_０から波が拡がって出て行きますが、波の山の位置はS₀を中心にした半球状になります。この球面波は玉ねぎのように次々と繰り返されて、Ｓ_１とＳ_２では、同じ球面が接します。このため、それぞれの穴からまた２次的に球面波が同じタイミイング（位相）で生まれて出て行きます。そして、壁の上の点Ｐで、それぞれの波の山が重なれば明るく、打ち消し合えば暗くなって、いわゆる干渉パターンが現れます。しかし、二つの波の位相の差（山の位置のずれ）がでたらめだと、干渉パターンが位相差の変化に応じて干渉パターンの位置がずれるので、これらが重なって見かけパターンは見えなくなります。大切なことは二つの波の位相差が変わらなければパターンが見えることです。もっとも、その時はスリットS_０はいらなくなります。後の話では、そのような二つの光源を用意することが話題になります。

S_０から出てくる光が弱くて、フォトン一個が飛ん出てくるような場合でも同じですが、そのフォトンがＳ_０からＰ点に届いたとき、どちらのスリットを通過したかは分かりません。ここがミソなのです。

同様のことはド・ブロイが考えたように、電子やそのほかの量子の場合にも起こります。そこで、S_１かS_２のどちらかの穴を塞ぐと、干渉パターンは見えなくなります。この現象はS_１とS_２から出てくる波動関数をΨ_１とψ_２と書けば、四角で示した領域の中の波動関数は、両者の和になります。そして、干渉パターンが安定に現れる場合は、二つの波の位相があっているといい、波動関数のコヒーレントな和として、四角の中では、波動関数は「重ね合わせ」の状態にある（エンタングルメントにある）と呼ばれます。

そのような状況を前提として、例えば、S_１から出る波動関数を「生きた猫」、S_２からの波動関数に「死んだ猫」で、重ね合わされた波動関数を「変な猫」といっているわけです。ですから、この猫は四角で囲んだ部屋にいて、誰かが覗くことは、一方のスリットを塞ぐことに相当し、その時は、干渉パターンが消える、つまり「変な猫」が消えるというわけです。

このような現象は量子力学の波動関数に限らず、一般の波に共通に起きるもので、波動方程式の複数の解を足し合わせても、もとの波動方程式の解になっているという数学的な性質（線形性）」によります。量子力学の波動関数は複素数の数で、その絶対値が猫の存在確率となりますので、その様子が神様の腕の振るいどこです。なお、普通の数の計算で、(a+b)²=a²+b²とはなりませんが、その違う分が干渉パターンが見える原因になるといえます。

次に「変な猫」に安全なパスワードを作ってもらうにはどうすればいいかを考えます。

まずは、どこからかそんな猫を探してこなくては話になりません。

注：ここで大方は素通りしてもいいことですが、すこし混乱させるようなことを補足しておきます。フォトンの波動関数として、シュレーディンガー方程式の解みたいなこと述べていますが、実は、電子のような場合はいいのですが、フォトンの場合は本当は違います。しかし、基本的なところの特徴は似ている部分もあり、実際の実験ではフォトンを使った研究がほとんどです。その意味では、今のところ、量子暗号といっても、フォトン暗号ともいえるもので、光通信技術の一部だといえます。なお、フォトンの波動関数の考え方について、少し専門的ですが北野正雄氏の解説があります。興味のある方はご覧ください。