３４　JR福知山線の電車脱線事故

2005年4月25日（月）JR西日本、福知山線塚口駅 - 尼崎駅間の右カーブ区間で、宝塚発、同志社前行き上り快速が脱線し、多くの通勤通学客が死傷した大事故が起きました。ここでまず、この事故で犠牲になられた死傷者の方々、その御家族など関係者の皆様に哀悼やお見舞いをあらためてさせて頂いた上で、この事故の原因の物理的側面をここでとり挙げることをお許しいただこうと思います。

その理由は、この電車の運動で起きた物理現象は、電車のみならず、物体が回転するときに物体が感じる遠心力や、原子の中の電子のミクロな運動によって発生する磁場や電子による光学過程を理解する上で決定的に重要だからです。

この電車は、急カーブを高速で通過する時に発生する遠心力に、レールと車輪が耐えられず脱線して、接線方向にまっすぐに飛び出し、その先にある建物に激突、車両が乗客もろとも押しつぶされてようやく止まりました。

車両が脱線して接線方向にまっすぐに飛び出しているのは、慣性の法則によるもので、この運動の「止めにくさ」は、次の式で表される質量ｍと速度ｖの積の「運動量」です。

一方、その運動量を持った電車の「曲がりにくさ」を表す量があり、これは「角運動量」と呼ばれて次の式で表現されます。　

すこし詳しくはこちら。

この量は、回転面に対して垂直を向いたベクトルで表され、回転の中心からの距離ｒと速度ｖを表すベクトルの方向とは、図のようになっています。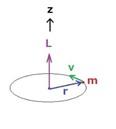今の場合、ｍは電車の車体と乗客などすべてを合わせた質量（簡単のために先頭車両だけを考えます）で、ｒはカーブの回転中心から脱線した車輪までの距離、ｖはその時の電車の走行速度です。

脱線の瞬間に先頭車両全体の持っていた全エネルギーは次の式でおおよそ表せます。、右辺第１項は運動エネルギー、２項が遠心力を生むポテンシャル、第３項はレールが車輪を押し返す復元力のポテンシャルです。

似た例としてハンマー投げの場合を考えますと、選手は最初に出来るだけ回転速度を上げるように自ら回転し、鉄の玉にかかる遠心力をロープと筋肉で支え、その限界付近で手を放して鉄の玉を前方に飛ばします。この場合、鉄の玉を回転中心へ引き戻すロープと筋肉に生まれる復元力のポテンシャルが、U（ｒ）になります。
イラスト：ぷにつく

同様なことは太陽の周りをまわる惑星の運動の場合にもあり、この場合Ｕ（ｒ）は万有引力によって太陽に引き寄せられるポテンシャルです。また、原子の中の電子の場合は、このポテンシャルはクーロン引力のポテンシャルになります。

そこで、運動エネルギーを除いた部分をひとまとめにした、実質的に働くポテンシャル（有効ポテンシャル）と考えて、次の式で表しますと、回転半径ｒ関数としておよそ次の図のようになります。

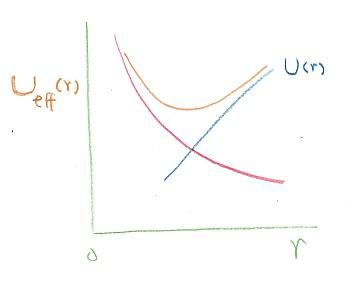
青の曲線は物体を回転中心（ｒ＝０）へ引き寄せる（ｒを短くする）ポテンシャル、赤の曲線は物体を回転中心から引き離す（ｒを長くする）ポテンシャルで、併せた有効ポテンシャル（オレンジ色の曲線）が最も低くなる位置で物体は安定に回転します。有効ポテンシャルはrの関数ですから、この場合は角運動量Lは変わりません（角運動量が保存する）ので、速度が遅いと有効ポテンシャルが最低になるｒは長くなります。

ところが、このバランンスが崩れて電車が脱線してレールから離れると、もう車体を引き戻す力がなくなるので、車体はｒが大きい方へと動いて、あとは慣性の法則に従って直進してしまいます。沢山の乗客を積んだ車体の重さは相当なもので、それが走行速度とほぼ同じ速さで進む上、動かない建物に衝突して短時間で止まるので、そこで働く力は莫大になり、何もかもが瞬間に圧搾されるという悲惨な状況が起きてしまったわけです。

上の関係式からわかるように、遠心力は、ｒが小さいほど、また、ｍやｖが大きいほど強くなります。

この事故の場合、ｒやＵ（ｒ）はレールの地形的、技術的制限から通常は十分な安全性を考慮して設計されているはずで、これが不適当だったなら同様な事故が同じ場所で多発していたはずで、この時だけというのはあり得ないでしょう。また、ｍはよほどの定員オーバーをしていなければ問題なさそうです。残るはｖですが、これは運転手や速度制御装置の問題となってしまい、物理学からは離れてしまいます。ただ、このような事故を避けるもっとも常識的で簡単な方策は、電車を徐行させることに他なりません。