３５　水素原子の電子の軌道

水素原子の中では電子はとても狭い空間で運動するために、その運動はシュレーディンガー方程式の解として得られる波動関数を基に、確率的にしか分からないことはすでに述べました。

そのため、３４で述べたようなニュートンの運動方程式で予想できるような、電子が陽子の周りを軌道を描いて周回するような考えではうまく説明ができません。実際には電子の運動は陽子を中心として３次元的に広がっているので、その波動関数は極座標を使って表現するのがふさわしく、陽子から測った距離ｒの関数である　と、角度だけに依存する部分の積で表現できることが方程式の数学的性質からわかっています。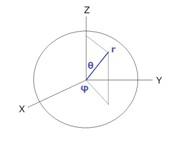

そして、　についての方程式では、次の数式で表せる有効ポテンシャルが得られることが知られています。
これを３４で述べた有効ポテンシャル　　　と比べると、右辺第1項が遠心力を生むポテンシャルに相当することが予想できます。

つまり、この場合は角運動量に関係する部分が　となっていることが分かります。ここで、ｌ＝０，１，２，・・の整数です。この関係は角度に関係する波動関数　の数学的要請から出てくるのですが、物理的な意味はこのままではよくわかりません。しかし、量子力学では角運動量が　であることが非常に重要な意味をもっていることがあとで分かります。とはいえ、角運動量というからには何か軌道運動を意味しているように思えるのですが、波動関数を求めてみてその関数の形から直観的に想像するのは慣れなければできません。

波動関数から、どのように軌道というイメージを想像すればいいのでしょう。

シュポルスキー（Eduard Vladimirovich Shpolsky,1892-1975）著、邦訳玉木英彦他３人『原子物理学』（東京図書）に、この関係がわかりやすく説明されています。（筆者の手元にある版は学生時代に入手した１９６２年５月の６刷り版です）この教科書の邦訳版の第２巻にその様子が図で示されています。しかし、筆者の持っている版では印刷が不鮮明なので、その一部を拡大して、必要な部分に色付けしたのが次の図です。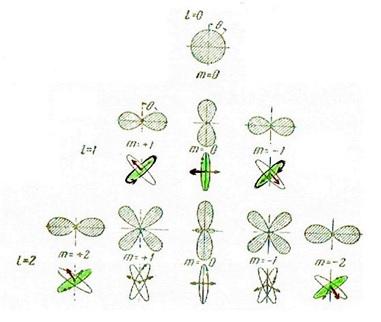

この図ではシュレーディンガー方程式の解として得られる水素原子の電子の波動関数から計算できる、電子が観測できる確率の高い領域が描かれています。この図では上向きがz軸を表し、θはz軸から測った角度です。（地球での緯度は赤道から測った角度としますが、ここではθは北極から測かった角度です）

上の段がｎ＝０、次がｎ＝１かつｌ＝１、一番下の段がｎ＝２かつｌ＝２の電子状態が例として描かれています。

ｎ＝１、ｎ＝２、ｎ＝３の状態は慣習としてｓ、ｐ、ｄ状態と呼ばれますが、これらの名前は関係する分光スペクトル線が、鋭い（sharp）、主に現れる（principal）、ボヤっとしている（diffuse）という事情から付けられています。

なお、電子が観測される確率の高い領域は、これらのパターンをz軸の周りで３６０度回転したものになり、最低エネルギーのｓ状態の電子は、陽子の周りに球状に拡がって運動しているので、軌道というような考えは成り立たちません。

次に中段に描かれたｐ電子では、左側の図では右回り、右側は左回りに電子は運動しています。したがって、敢えて衛星の運動のような軌道面を草色のように対応させると、角運動量はｚ軸に対して４５度傾いています。その様子を右の図に示しました。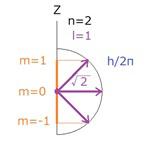

このように量子力学では、角運動量の向く方向が特定の方向に制限されているのが特徴で、これは方向の量子化と呼ばれ、エネルギーの量子化と合わせて量子の世界の特徴となっています。

上で述べたように波動関数の空間的な形はz軸の周りに３６０度回転した３次元的なものですから、角運動量のベクトルもｚ軸の周りで特定Φで固定されているものではないので、実際はz軸に垂直な成分は平均して打ち消され、z軸に沿った分だけ、つまり角運動量のｚ成分だけが平均して値を持っていることが予想でき、理論的にも証明できます。なお、ｍは方向の量子化を表す指数で、ここでは軌道面の傾きを表現しているという風に考えておくことにします。

さて、下段のｄ電子の場合は、例えば左端と右端では、ｐ状態に比べて角運動量の傾きがz軸に近くなっています。

もっとｎが大きくなると、ｌとｌ＋１の差がほとんどなくなり、軌道面はｚ軸に垂直に近づきますので、角運動量もニュートン力学で導かれるものに近くなります。これはｎが大きいと電子のエネルギーが大きくなるので、運動する領域も陽子から離れた広い領域に拡がり、電子の位置の不確定度が増すので、その分速度の曖昧さが少なくなってある短い時間で電子が特定の場所で観測される確率の空間分布がはっきりしてくるためです。
一般に、あるlに対して、ｍは-lからlまで2l+1種類あります。従って、一つのｎに対して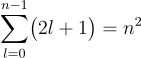だけのｍの値があることになります。　例えば、n=2に対しては4種類のエネルギーの同じ状態があります。（このような状態を縮退していると呼ばれます）実際はもう少し複雑です。量子力学では、ｎ、ｌ、ｍをそれぞれ「主量子数」、「方位量子数」、「磁気量子数」と呼ばれます。

これらの量子数を使ってシュレーディンガー方程式から得られる水素原子の電子のエネルギーを表現すると、次のようになります。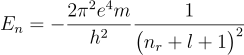
これは前に示した電子のエネルギー、　の分母をと置き換えたものになります。の最小値は０ですから、ｎが最小になるにはが０でなくてはなりません。また、ある決まったｎに対するの最大値はn-1になります。従って、あるｎに対しては０からn-1まであることになります。

以上のように量子力学で水素原子の電子の運動を考えると、電子の軌道運動のイメージがよく分からないように思えますが、このように詳しく見れば、陽子の周りで軌道運動をしている様子が推測できます。ただ、上で述べたことですが、最低のエネルギーの１ｓ状態の電子は陽子を中心として球状に確率分布が拡がっているので、軌道運動というイメージはなくなっています。

注：量子力学の教科書では、角運動量にかかわる観測可能な量（物理量と呼ばれる）を波動関数に数学的な演算を行う作用素（オペレーター）の期待値という抽象的な概念を使って説明するのが普通です。しかし、実際の物理量を作用素に対応させることは数学的には便利ですが、抽象的で実態が見え難い難点があります。もっと直感的に波動関数の幾何学的な形から電子の運動形態を予想して、それから類推できる角運動量の実態が想像できれば、惑星の運動（古典力学）における角運動量と、量子の運動（量子力学）における角運動量との一見大きく違うようにみえる様子も、筋道だって考えれば違和感なく理解できるのではないかと思いましたので、ここでは敢えて通常の作用素使った扱いには触れませんでした。