３６　ミクロの磁石

カーブした道を進む車に乗って方位磁針を見ていると、針はいつも北を向くように回転します。これは地球が永久磁石になっていて、磁場が南から北へ向かっているので、方位磁針が絵のように地球の磁場に平行になるように回転するからです。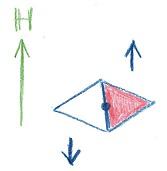この回転をさせる力は偶力（トルク）と呼ばれ、次のようなベクトルで表されます。　ここでは磁気モーメントと呼ばれるベクトル量で、磁石の強さをあらわします。この掛け算のX印は、普通の数の積ではなく、ベクトル積（直積）を表します。

次の絵は方位磁針のかわりに、一重のコイルを置いて電流を矢印の方向に流した様子です。やはり絵のようにトルクが発生してコイルは回転します。電流を流して回転させるのが電動モーター、外部の装置で軸を回転させて電流を発生させるのが発電機です。この場合は電流をI、面積をSとすると、磁気モーメントは次の式で表されます。

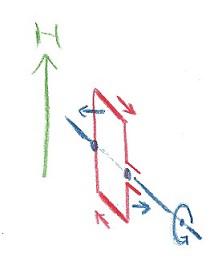
ここでコイルのかわりに水素原子の中で軌道運動をする電子に置き換えてみましょう。量子力学ではこの電子の軌道運動は惑星の場合と違いますが、前に述べたように何かしらの軌道めいた形でマイナスの電荷が運動しているので、コイルに電流が流れているような考え方ができます。

コイルの場合は電流にコイルの断面積を掛けた量が磁石の強さに比例するという考え方は実用上便利ですが、原子の電子の場合はこの考えをそのまま応用するのは筆者はあまり気が進みません。むしろ、電流は電子の流れだという基本に戻って、この場合のトルクや磁気モーメントを考えてみました。

少し詳しくはこちら。

電子の軌道の半径をｒ、電子の速度をｖ、電荷をーeとして、トルクは次の式で表されます。ここでLは角運動量です。

この式を最初に示した式と比べると、磁気モーメントがであることがわかります。

次に電子が磁場から受けるエネルギーは、トルクによって磁場が電子にする仕事Wですから、次の積分を計算すると求まります。　実際の計算は次のような量を計算することになり、電子が感じる磁場中でのポテンシャルエネルギー、つまり電子と磁場との相互作用のエネルギーが得られます。

この場合のとの積はスカラー積（内積）と呼ばれ、「・」印で表します。

今、磁場の強さが空間的にも時間的にも変化しないとすると（一様な静磁場と呼ばれます）、磁気モーメントの磁場方向（ｚ軸方向と決めますと）の成分の大きさと磁場の大きさの積が＋の場合には、ポテンシャルは－になりますので低くなり、逆の場合に比べて電子はより安定になります。また、磁気モーメントと磁場の方向が直角の場合には、このポテンシャルの影響を電子はうけません。したがって、静磁場の中では角運動量をもっている電子のエネルギーは分裂し、その程度は磁場の強さに比例して大きくなります。

この現象は、オランダの物理学者ゼーマン(Pieter Zeeman, 1865-1943）が１８９６年に発見したもので、以来彼に因んでゼーマン効果と呼ばれています。

軌道角運動量が０のｎ＝１の電子には軌道面というものがありません。したがって、角運動量はゼロなので磁石にはなれず、エネルギーが磁場によって分裂することは予想できません。ところが事実に反してｓ電子のエネルギーも２つに分裂します。何故でしょう？　

これは電子をはじめ、量子にはスピンと呼ばれる量子の持つ不思議な性質の表れの一部です。このために色々な原子についての分光学的な測定によれば、電子のエネルギーの磁場による分裂は非常に複雑です。これは軌道運動によって生まれる磁石と、電子自身もつスピンによる磁石との組み合わせの効果によるものです。このあたりは量子力学での重要な事項の一つで、教科書や講義では詳しい説明がされます。また、一般に物質の磁性をミクロに理解し、応用する上で非常に重要です。しかし、専門的になり過ぎるますので、ここでは扱わないことにしました。

なお、ゼーマン効果の発見ついては、A J Kox による、“The discovery of the electron: II. The Zeeman effect ”がわかりやすい説明があります。https://pure.uva.nl/ws/files/3655500/2775_26336y.pdf