３８　パウリの排他律

３７節で述べたように、軌道角運動量を持たないs電子もスピンという量子が一般に備えている固有の性質による角運動量を持っていることがわかりました。

この性質はスピンと呼ばれますが、これは陽子、中性子、そして電子というわずか三種類だけの基本粒子の組み合わせの違いだけによって化学的にそれぞれ違った１１８種類の元素ができていることを説明する上で決定的な役割を演じています。

これを決めているのは「パウリの排他律」と呼ばれる経験則です。ですから、私たちがいること、また宇宙の現在の姿が実現している事実はこの規則のおかげです。水素の最低のエネルギーを持つ電子の状態を例にこの規則をみてみましょう。

水素原子のエネルギーは、最低のエネルギー状態はｎ＝１，ｌ＝０、ｍ＝０です。これに加えてスピンによる磁気量子数±１/2の二通りがあり、磁場のない時には同じエネルギーです。しかし、少し考えると次の絵のように３種類があってもいいように思います。ところが実際には、この二つの状態を同じ向きのスピンが共存することはできないことが発見されました。この禁制がパウリの排他律です。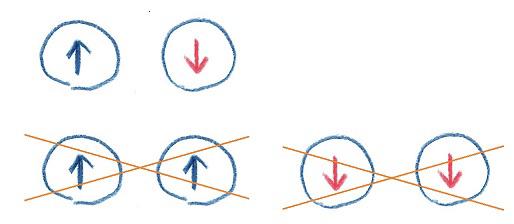
水素には一個しか電子はいませんから、そのスピンの向きを絵のように上向きと下向きの矢印で示したときに、一個の電子がどちらのスピンをもっているかはあらかじめ決まっているわけではなく、上向き状態と下向き状態は、シュレーディンガーの猫の例えで言えば、一方が死んだ猫、もう一方が生きた猫で、３７で紹介したような観測が行われないかぎり、二つの状態は「変な猫」といってきた重ね合わせ状態になります。つまり、３７で紹介した不均一磁場の中を通すという実験によって、測定のたびに電子の曲がった方向から、スピンがどちらとして観測されたかがわかったことになります。

パウリの排他律によって、ｎ＝１の電子状態だけでなく、すべての一組の（ｎ、ｌ、ｍ）で決まる電子のエネルギー状態を持つことができる電子は反対のスピンをもった一対だけになります。この状況は劇場の最前列にペアの席があり、上の段に昇るほどペアの席は増えますが、そのどこが電子で埋まっているかは、個々の原子核の陽子の数に等しい電子の数で決まるのですが、最前列から順番に座って、ある段の席が全部埋まれば、ヘリウムやネオンなどの希ガス原子、その上の段が一つしか埋まっていない原子が、リチウム、ナトリウムなどアルカリ原子というわけです。この様子を整理したものが周期律表です。

この規則を発見したのは、オーストリア・ウイーン育ちのW.パウリ（Wolfgang Ernst Pauli、1900-1958）です。

彼は18歳の頃すでにアインシュタインの相対論をマスターし、1921年にドイツのA.ゾンマーフェルトの下で学位をとり、彼の依頼によってその直後に有名な相対論の教科書を書いたという凄い人物です。彼はこの排他律の発見によって1945年、ノーベル物理学賞を授与されましたが、その講演録にはこの規則を彼が見つけた経緯が述べられています。

彼がドイツのミュンヘンのゾンマーフェルトの下で研究し始めた頃のこと、そのグループでは、ロシアの化学者メンデレーフ（Dmitrij Ivanovich Mendelejev,1834-1907）が1869年に発表した周期律とリュードベリーが1890年に提案した原子スペクトルに現れるスペクトル系列の規則性との関係が熱心に議論されていたそうで、この議論に大いに影響されたそうです。更にボーアの原子モデルにも刺激されて、パウリは自身のアイデアをまとめて１９２４年に排他律として発表しました。ゼーマン効果の発見が１８９６年、シュテルン・ゲルラッハの実験が１９２１年なので、これらの実験は彼がこの理論を発表する前ですので、これらも大きく参考になったはずです。

筆者が量子力学を知ったころ、パウリの理論がド・ブロイの理論が発表されたのと同じ年だったことや、その翌年にすでにスピンという名前が世にでたこと（しかし、その時は電子の自転のようなイメージで使われていたようで、現在の考え方ではそのようなイメージは意味がないことがわかっています）という歴史的な順序については気づいていませんでした。

実は、シュレーディンガーの理論はパウリの理論が発表された２年後だったのです。

因みに、P.デラック（Paul Adrien Maurice Dirac, 1902-1984）によって、スピンの存在が相対論を考慮した波動方程式によって理論的に裏付けられたのは、更に4年後のことです。

ですから、パウリは、今日のスピンという言葉ではなく、電子の持つ「classically non-describable two-valuedness、（古典論では説明できない二価性）」と呼んでいました。

読者はお気づきのように、電子は量子ですから「のっぺらぼう」の仲間です。しかし、フォトンの場合は、無限の数のフォトンが同じエネルギー状態を持つことができました。ところが電子の場合はそうではなかったのです。

つまり、「のっぺらぼう」には二種類があることがわかります。経験的には、スピンが半整数の「のっぺらぼう」にはパウリの排他律が成り立ち、整数の場合にはパウリの排他律は適応されません。

前者はフェルミオン、後者はボソンと呼ばれます。これも経験的な事実ですが、ボソンの場合は交換によって波動関数の符号は変化しませんが、フェルミオンの場合は符号が変化します。専門的になるので、この例など詳しいことはここでこれ以上は触れないことにしました。

とにかく驚くべきことは、この二種類の「のっぺらぼう」によってこの宇宙ができていることです。

前に述べたように、パウリの排他律は経験則であり、この本質についてパウリ自身も懐疑的だったそうです。つまり、なぜこんな規則があるのか、その本質的な理由は現在もわかっていません。

そうだったら、一つぐらいこの禁制が崩れる例が見つかってもいいじゃないか？　そうに思うのも人情です。

実際それを探す実験を行っている研究者たちがいます。筆者はこのような実験にとても魅力を感じます。

２０１８年にイタリアのグラン・サッソの国立研究所の地下（Laboratori Nazionali del Gran Sasso; LNGS）でその実験が行われてきました。

右の図は、パウリの排他律の例外が見つかる確率(縦軸の値)が、実験を重ねるほどに精度が高まり小さくなっている様子を時系列で示したものです。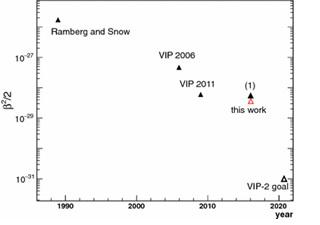

この論文の実験（赤の△）ではその確率を表す指数が１０^－２７程度であったとし、更に3桁少ないことを実証することを目指すと書かれています。実際2020年の論文では1/2β2<1.53·10⁻⁴³ となっています。

このデータを見れば確かにこの排他律の厳密さ、凄さが感じられます。どの辺で、もうこれぐらいでいいことにしようと研究が打ち切られるのかはわかりませんが、筆者はどこまでも続けてほしいと思います。

なお、この研究所では、この実験だけでなくそのほかの実験にも、ローマ時代の鉛が放射線の遮蔽材として使われるということです。というのもローマ時代の鉛の水道管や貨幣が遺跡の発掘で出土されています。この鉛は精密な実験の邪魔になるバックグラウンドの放射線量を減らす遮蔽材として使われているそうです。というのも、鉛に含まれているウランなどによる放射崩壊による放射線の量が、年月が経っているので少ないからだそうです。イタリアならではの話ですが、ただ、問題もあって、考古学者は貴重な出土品だから鋳つぶして使ってくれるなというし、物理学者は自然の真理を解くためだから使う価値があると主張して議論になっているそうです。

両者の折り合いがついて面白い異分野間の交流が生まれるのは、将来の意外な発見につながるのではないかと思います。