３９　フォトンのスピン

電子にはスピンという固有の角運動量が備わっていて、永久磁石のような性質を示すことがわかりました。

フォトンも量子です。では、やはりスピンを持っているのでしょうか？
フォトンのスピンは１で、統計的にはボソンと呼ばれる量子であることがわかっています。

でも、質量もないし、なにかの周りをまわるような姿もありません。水素原子の電子のような軌道運動による角運動量はなく、磁気モーメントもありません。

フォトンがスピンをもっていることはどのようにしてわかるのでしょう？

これを知るもっとも分かりやすい現象は、水素原子のｎ＝１の電子のゼーマン効果によって二つに分裂した電子状態の間に起きる光吸収過程です。

右の絵は、水素原子の１ｓ電子が磁場の中で二つに分裂する様子をスケッチしたものです。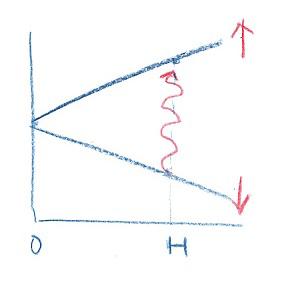磁場の方向をz軸とした時にスピンが磁場と反対の方向（絵の下向きの矢印）を向いた状態から、上向きの状態へ一個のフォトンを吸収して遷移します。電子の波動関数はどちらも偶関数ですから、方違いのときに紹介したような電子の分極が光の電場から力を受けると考えると、＜１ｓ｜eｒ｜１ｓ＞の積分は消えてしまいます。どうしてこの光遷移が起きるかというと、この場合はスピンによる磁石（磁気双極子）が、光の時間的に振動する磁場によって揺り動かされるという相互作用によるからです。

つまり、この相互作用は空間的には角運動量と同じ幾何学的性質を持っていて、惑星の運動についてのケプラーの第二法則として知られている面積速度一定という角運動量保存を表す現象と同じですから、面積は距離の二乗で偶関数です。そのため相互作用も偶関数になって、＜１Ｓ｜ｒ^２｜１Ｓ）となって積分が一般にはゼロにならないからです。

絵のように、この遷移ではスピンをー1/2から1/2へ変化させる（棒磁石の向きを逆にするようなものです）ので、これはフォトンがスピン１を持っていて、全体で角運動量が保存していることを意味します。

この場合のフォトンはマイクロ波の領域のフォトンになります。この吸収現象を利用したものがESR（電子スピン共鳴分光）といわれ、広く使われています。

これと似た現象で、核磁気共鳴（MNR）といわれる現象があります。これは例えば水素原子の原子核の陽子のスピンがやはり1/2であるために、磁場によって２つに分裂した状態間でフォトン一個が吸収される現象です。

これもフォトンのスピンが１であることを示しています。この場合は核磁気モーメントは電子の磁気モーメントの分母にある電子の質量の代わりに、およそ２千倍ほど大きい陽子の質量が入ったものになるために、ＥＳＲに使う磁場と同じ強さの磁場でも、分裂の大きさがその分小さくなるために、吸収されるフォトンは電波の領域の光のフォトンになります。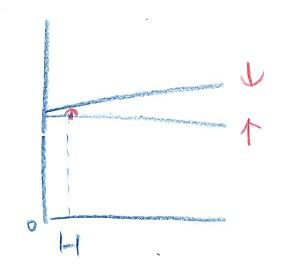その様子を右に絵で示しました。スピンの向きが電子と逆になっています。これは陽子はプラスの電荷を持っているために磁気モーメントが電子の場合と逆になるためです。

私たちに身近なMRIによる診断は、このフォトンのスピンが１であることをうまく利用したものなのです。

このようにフォトンのスピンが１であることは、普通の光の境域のフォトンでも同じです。その例として、水素原子の電子のｎ＝１からｎ＝２の状態への光吸収過程を見てみましょう。

次の絵は原子の運動エネルギーにｎ＝１とｎ＝２の電子のエネルギーを加えたエネルギーを縦軸に、陽子と電子の運動量を共通の運動量として横軸に誇張して描いたものです。原子の運動エネルギーのほとんどは陽子のもので、運動量に対して放物線になります。原子が止まっているときの電子のｎ＝１のエネルギーを原点にとっています。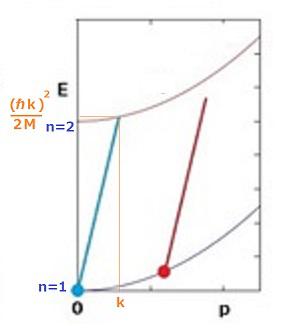

原子が真空中に止まっているとすると、フォトンのエネルギーと運動量の関係はですから、原子と同じ方向に進むフォトンのエネルギーがちょうどｎ＝２の電子状態になるときに、フォトンが電子に吸収されて消えます。このときエネルギーだけでなく、運動量も保存しますので、フォトンを吸収した原子はフォトンから運動量をもらって動きだします。その様子は緑の斜めの直線で表されます。この時、角運動量も保存されますので、ｎ＝１では軌道角運動量がゼロ、ｎ＝２では１ですから、フォトンの角運動量がやはり１であることがわかります。

さて、原子がある速度で動いていたらどうでしょう。その様子を赤い線で表しました。この線の長さは緑と同じですが、この場合はｎ＝２に届きません。つまり、原子が動いていると止まっているときとは違ったフォトンでないと効率よく吸収過程が起きないのです。

実際の気体では、原子は温度に応じていろいろな速さで動いています。そのために、このような一個のフォトンの吸収スペクトルは、止まっている原子の場合に比べて拡がっているように見えてしまいます。そこで、ｎ＝１とｎ＝２の電子のエネルギーの差を正確に知りたいときには、この方法では詳しく分かりません。

水素原子のように単純な原子の研究は、電子の軌道運動による磁石とスピンによる磁石との複雑な絡み合いによるエネルギーの変化、陽子のスピンによる磁石の効果、また電磁相互作用の詳しい繰り込み効果など、最初に考案されたシュレーディンガー方程式を解くだけでは分からなかった量子力学として基本的な問題を知るためには非常に重要で、もっと別の精密な分光法がないかと研究者たちは望んだのです。そこに、レーザーという今までになく強い新しい光源が開発されてので、この目的に開発されたのが、二光子分光です。

原子による二光子過程を一般的に初めて論じた論文は、マリア・ゲッパード（Maria Göppert-Mayer、1906-1972:後のゲッペルト・メーヤーで、原子核のシェルモデルによって１９６３年ノーベル物理学賞を与えられた学者です）がボルンの学生として１９３０年に博士論文としてまとめたものです。この光学過程はラマン効果なども含んだものですが、２光子吸収過程については当時レーザーのような光がなかったので、ながらく実用にはならなかったものです。

次の絵は、この方法では正しくｎ＝１とｎ＝２の電子のエネルギーを決められる様子を示しています。つまり、原子がどのように動いていても、前に例で示した止まった原子の一光子吸収が起きるフォトンのエネルギーの半分のエネルギーを持ったフォトン２個を向かい合わせに吸収させると、運動量は吸収する前と後で変わらないので、原子速度に関係なく、止まった原子の場合のように正しいエネルギー差が求まるわけです。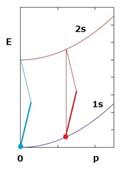

詳しくは省略しますが、この場合ｎ＝１とｎ＝２の角運動量はゼロの俗に１Ｓと２Ｓのエネルギーの差が求まります。どちらの状態も角運動量はゼロです。したがって、２個のフォトンの角運動量の和がゼロとなる必要があり、実際には右回りと左回りの円偏光が組み合わせられます。つまり、円偏光は光の進む方向に対して、右回りまたは左回りのトルクを電荷に与える電場ですから、それらが逆向きのトルクを与えるという意味で、角運動量が互いに逆となり、二つのフォトンの角運動量がゼロとなってこの吸収過程が起きるのです。
筆者はこの分光法に非常にお世話になりました。このことについては『励起子（exciton)の魅力』の中で話題にします。